Programming with Personalized PageRank: A Locally Groundable First-Order Probabilistic Logic
Paper and Code
May 10, 2013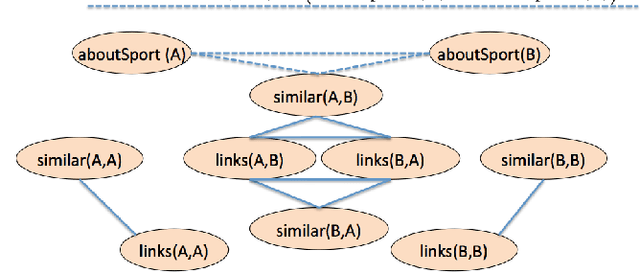
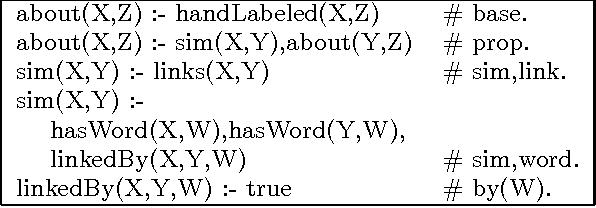
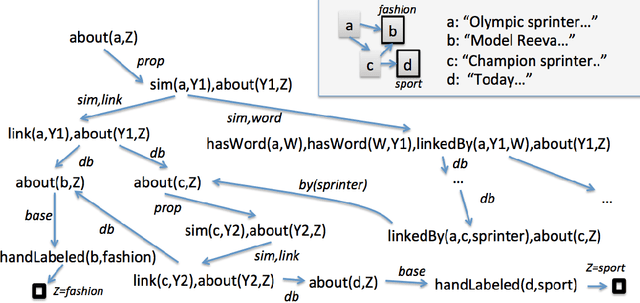
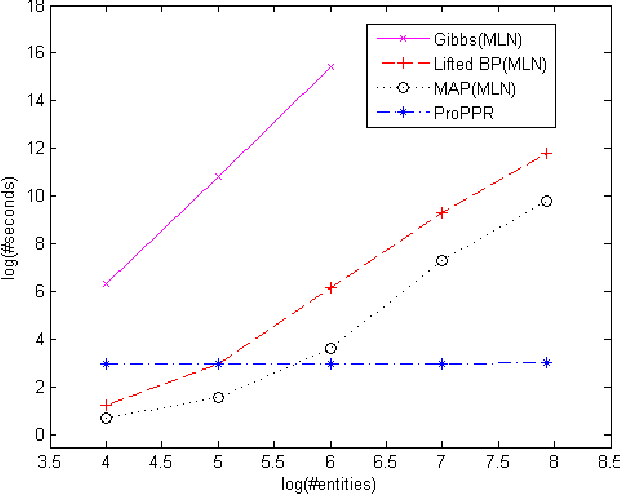
In many probabilistic first-order representation systems, inference is performed by "grounding"---i.e., mapping it to a propositional representation, and then performing propositional inference. With a large database of facts, groundings can be very large, making inference and learning computationally expensive. Here we present a first-order probabilistic language which is well-suited to approximate "local" grounding: every query $Q$ can be approximately grounded with a small graph. The language is an extension of stochastic logic programs where inference is performed by a variant of personalized PageRank. Experimentally, we show that the approach performs well without weight learning on an entity resolution task; that supervised weight-learning improves accuracy; and that grounding time is independent of DB size. We also show that order-of-magnitude speedups are possible by parallelizing learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge