Probabilistic Permutation Graph Search: Black-Box Optimization for Fairness in Ranking
Paper and Code
Apr 28, 2022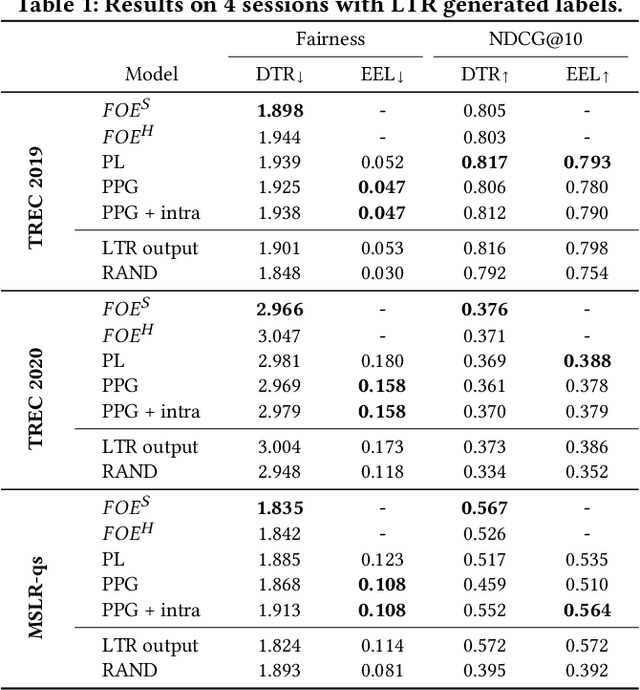
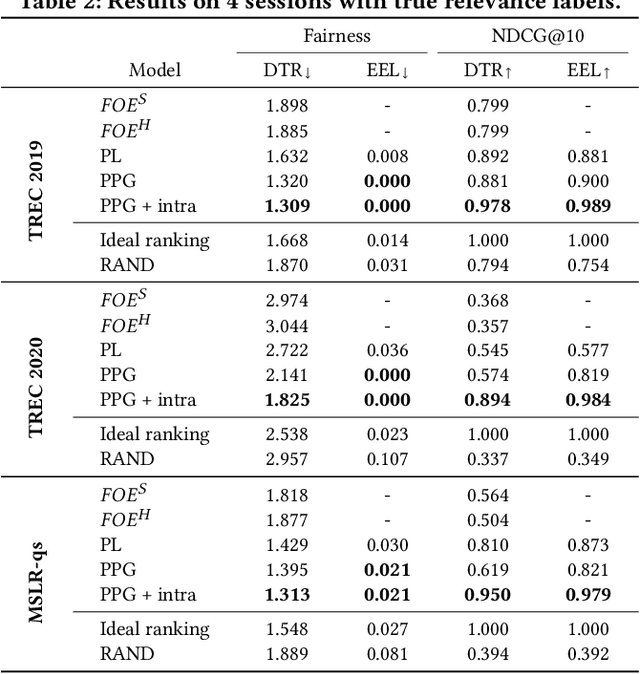
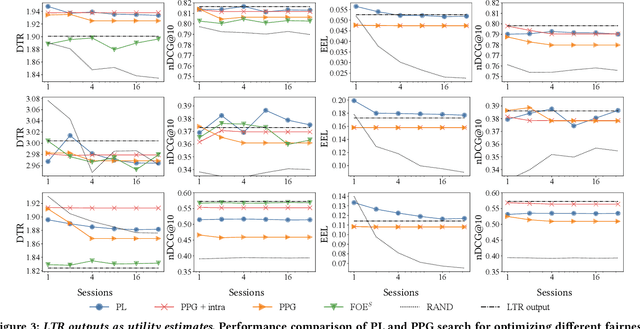
There are several measures for fairness in ranking, based on different underlying assumptions and perspectives. PL optimization with the REINFORCE algorithm can be used for optimizing black-box objective functions over permutations. In particular, it can be used for optimizing fairness measures. However, though effective for queries with a moderate number of repeating sessions, PL optimization has room for improvement for queries with a small number of repeating sessions. In this paper, we present a novel way of representing permutation distributions, based on the notion of permutation graphs. Similar to PL, our distribution representation, called PPG, can be used for black-box optimization of fairness. Different from PL, where pointwise logits are used as the distribution parameters, in PPG pairwise inversion probabilities together with a reference permutation construct the distribution. As such, the reference permutation can be set to the best sampled permutation regarding the objective function, making PPG suitable for both deterministic and stochastic rankings. Our experiments show that PPG, while comparable to PL for larger session repetitions (i.e., stochastic ranking), improves over PL for optimizing fairness metrics for queries with one session (i.e., deterministic ranking). Additionally, when accurate utility estimations are available, e.g., in tabular models, the performance of PPG in fairness optimization is significantly boosted compared to lower quality utility estimations from a learning to rank model, leading to a large performance gap with PL. Finally, the pairwise probabilities make it possible to impose pairwise constraints such as "item $d_1$ should always be ranked higher than item $d_2$." Such constraints can be used to simultaneously optimize the fairness metric and control another objective such as ranking performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge