Probabilistic K-means Clustering via Nonlinear Programming
Paper and Code
Jan 10, 2020
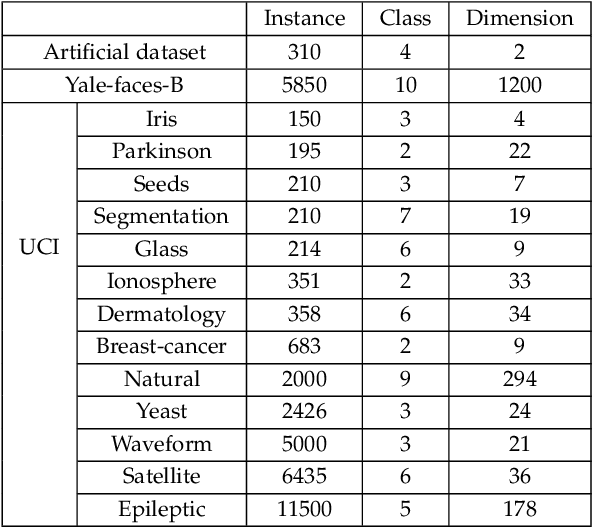
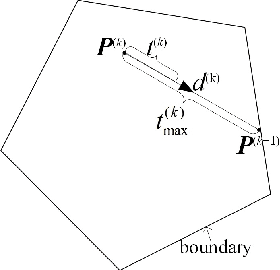

K-means is a classical clustering algorithm with wide applications. However, soft K-means, or fuzzy c-means at m=1, remains unsolved since 1981. To address this challenging open problem, we propose a novel clustering model, i.e. Probabilistic K-Means (PKM), which is also a nonlinear programming model constrained on linear equalities and linear inequalities. In theory, we can solve the model by active gradient projection, while inefficiently. Thus, we further propose maximum-step active gradient projection and fast maximum-step active gradient projection to solve it more efficiently. By experiments, we evaluate the performance of PKM and how well the proposed methods solve it in five aspects: initialization robustness, clustering performance, descending stability, iteration number, and convergence speed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge