Probabilistic Directed Distance Fields for Ray-Based Shape Representations
Paper and Code
Apr 13, 2024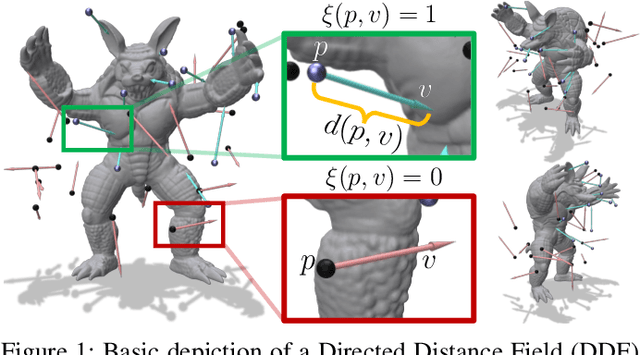

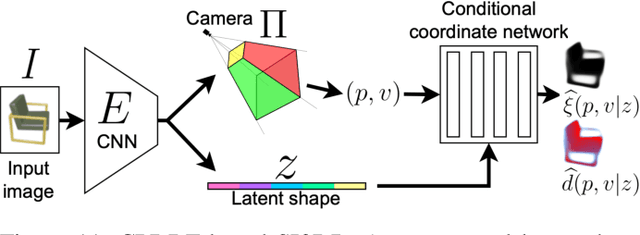

In modern computer vision, the optimal representation of 3D shape continues to be task-dependent. One fundamental operation applied to such representations is differentiable rendering, as it enables inverse graphics approaches in learning frameworks. Standard explicit shape representations (voxels, point clouds, or meshes) are often easily rendered, but can suffer from limited geometric fidelity, among other issues. On the other hand, implicit representations (occupancy, distance, or radiance fields) preserve greater fidelity, but suffer from complex or inefficient rendering processes, limiting scalability. In this work, we devise Directed Distance Fields (DDFs), a novel neural shape representation that builds upon classical distance fields. The fundamental operation in a DDF maps an oriented point (position and direction) to surface visibility and depth. This enables efficient differentiable rendering, obtaining depth with a single forward pass per pixel, as well as differential geometric quantity extraction (e.g., surface normals), with only additional backward passes. Using probabilistic DDFs (PDDFs), we show how to model inherent discontinuities in the underlying field. We then apply DDFs to several applications, including single-shape fitting, generative modelling, and single-image 3D reconstruction, showcasing strong performance with simple architectural components via the versatility of our representation. Finally, since the dimensionality of DDFs permits view-dependent geometric artifacts, we conduct a theoretical investigation of the constraints necessary for view consistency. We find a small set of field properties that are sufficient to guarantee a DDF is consistent, without knowing, for instance, which shape the field is expressing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge