Principal Word Vectors
Paper and Code
Jul 09, 2020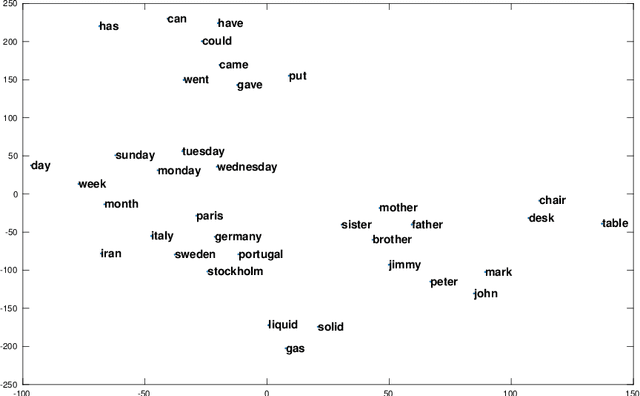

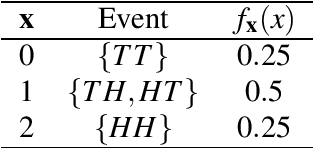
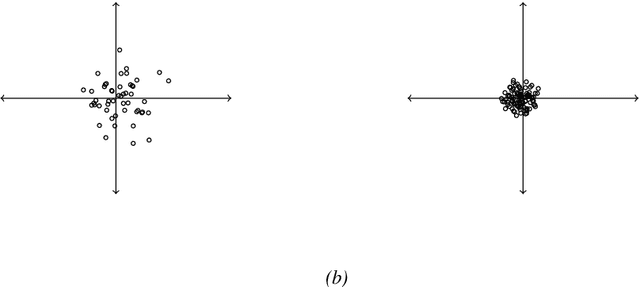
We generalize principal component analysis for embedding words into a vector space. The generalization is made in two major levels. The first is to generalize the concept of the corpus as a counting process which is defined by three key elements vocabulary set, feature (annotation) set, and context. This generalization enables the principal word embedding method to generate word vectors with regard to different types of contexts and different types of annotations provided for a corpus. The second is to generalize the transformation step used in most of the word embedding methods. To this end, we define two levels of transformations. The first is a quadratic transformation, which accounts for different types of weighting over the vocabulary units and contextual features. Second is an adaptive non-linear transformation, which reshapes the data distribution to be meaningful to principal component analysis. The effect of these generalizations on the word vectors is intrinsically studied with regard to the spread and the discriminability of the word vectors. We also provide an extrinsic evaluation of the contribution of the principal word vectors on a word similarity benchmark and the task of dependency parsing. Our experiments are finalized by a comparison between the principal word vectors and other sets of word vectors generated with popular word embedding methods. The results obtained from our intrinsic evaluation metrics show that the spread and the discriminability of the principal word vectors are higher than that of other word embedding methods. The results obtained from the extrinsic evaluation metrics show that the principal word vectors are better than some of the word embedding methods and on par with popular methods of word embedding.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge