Primal-Dual Spectral Representation for Off-policy Evaluation
Paper and Code
Oct 23, 2024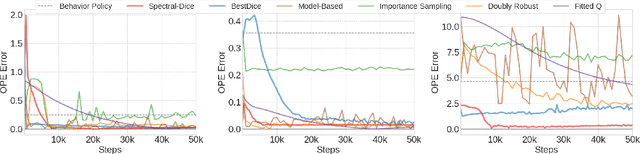
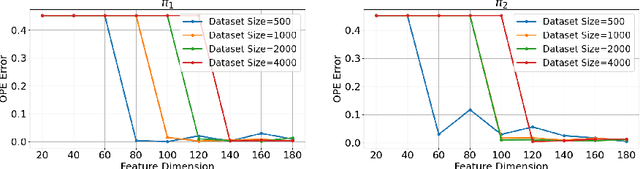
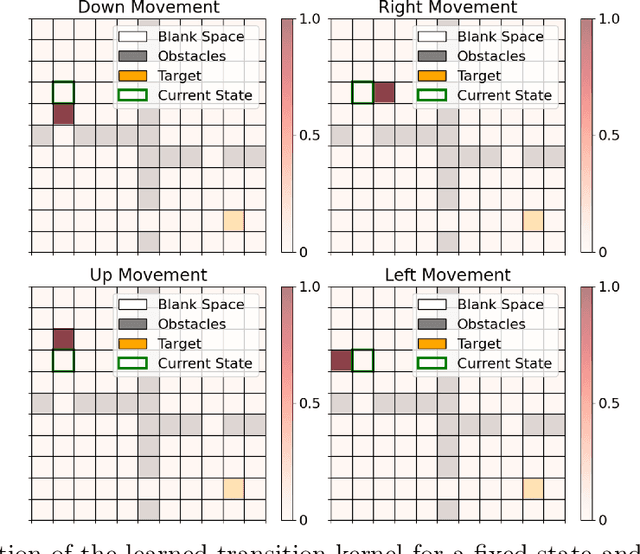
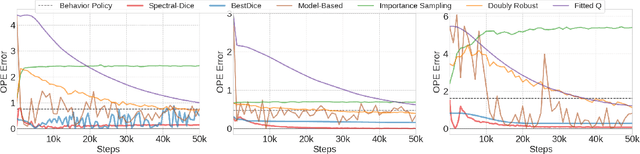
Off-policy evaluation (OPE) is one of the most fundamental problems in reinforcement learning (RL) to estimate the expected long-term payoff of a given target policy with only experiences from another behavior policy that is potentially unknown. The distribution correction estimation (DICE) family of estimators have advanced the state of the art in OPE by breaking the curse of horizon. However, the major bottleneck of applying DICE estimators lies in the difficulty of solving the saddle-point optimization involved, especially with neural network implementations. In this paper, we tackle this challenge by establishing a linear representation of value function and stationary distribution correction ratio, i.e., primal and dual variables in the DICE framework, using the spectral decomposition of the transition operator. Such primal-dual representation not only bypasses the non-convex non-concave optimization in vanilla DICE, therefore enabling an computational efficient algorithm, but also paves the way for more efficient utilization of historical data. We highlight that our algorithm, SpectralDICE, is the first to leverage the linear representation of primal-dual variables that is both computation and sample efficient, the performance of which is supported by a rigorous theoretical sample complexity guarantee and a thorough empirical evaluation on various benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge