Prevention is Better than Cure: Handling Basis Collapse and Transparency in Dense Networks
Paper and Code
Aug 22, 2020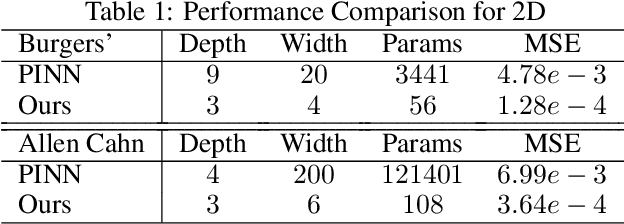
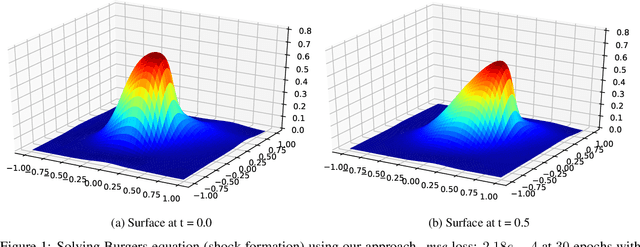
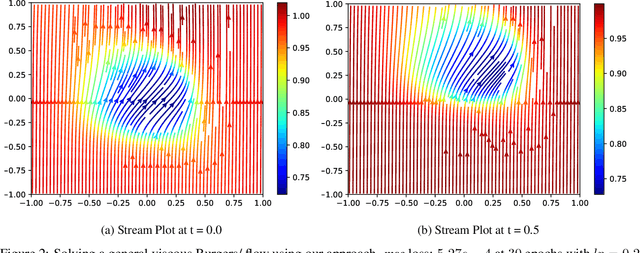
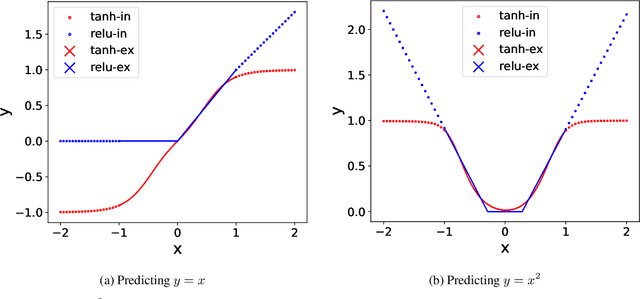
Dense nets are an integral part of any classification and regression problem. Recently, these networks have found a new application as solvers for known representations in various domains. However, one crucial issue with dense nets is it's feature interpretation and lack of reproducibility over multiple training runs. In this work, we identify a basis collapse issue as a primary cause and propose a modified loss function that circumvents this problem. We also provide a few general guidelines relating the choice of activations to loss surface roughness and appropriate scaling for designing low-weight dense nets. We demonstrate through carefully chosen numerical experiments that the basis collapse issue leads to the design of massively redundant networks. Our approach results in substantially concise nets, having $100 \times$ fewer parameters, while achieving a much lower $(10\times)$ MSE loss at scale than reported in prior works. Further, we show that the width of a dense net is acutely dependent on the feature complexity. This is in contrast to the dimension dependent width choice reported in prior theoretical works. To the best of our knowledge, this is the first time these issues and contradictions have been reported and experimentally verified. With our design guidelines we render transparency in terms of a low-weight network design. We share our codes for full reproducibility available at https://github.com/smjtgupta/Dense_Net_Regress.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge