Predictive Coding Can Do Exact Backpropagation on Any Neural Network
Paper and Code
Mar 08, 2021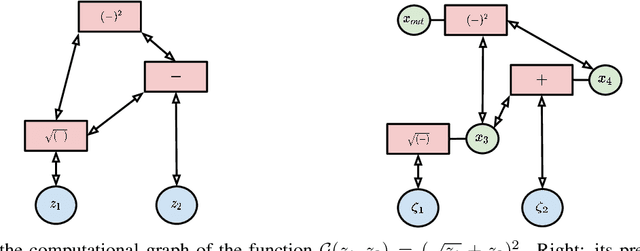
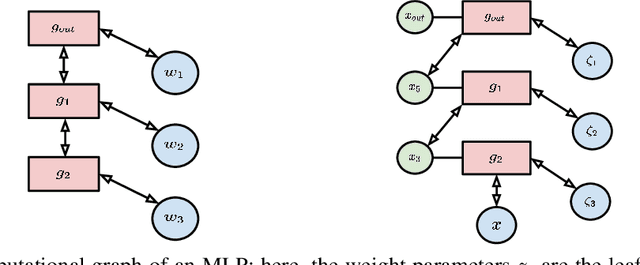

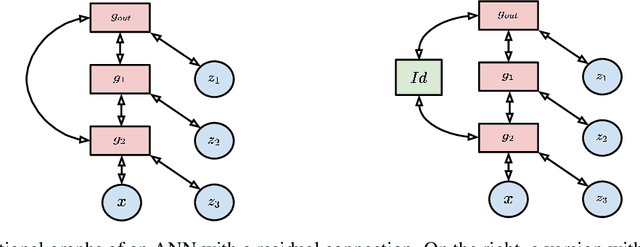
Intersecting neuroscience and deep learning has brought benefits and developments to both fields for several decades, which help to both understand how learning works in the brain, and to achieve the state-of-the-art performances in different AI benchmarks. Backpropagation (BP) is the most widely adopted method for the training of artificial neural networks, which, however, is often criticized for its biological implausibility (e.g., lack of local update rules for the parameters). Therefore, biologically plausible learning methods (e.g., inference learning (IL)) that rely on predictive coding (a framework for describing information processing in the brain) are increasingly studied. Recent works prove that IL can approximate BP up to a certain margin on multilayer perceptrons (MLPs), and asymptotically on any other complex model, and that zero-divergence inference learning (Z-IL), a variant of IL, is able to exactly implement BP on MLPs. However, the recent literature shows also that there is no biologically plausible method yet that can exactly replicate the weight update of BP on complex models. To fill this gap, in this paper, we generalize (IL and) Z-IL by directly defining them on computational graphs. To our knowledge, this is the first biologically plausible algorithm that is shown to be equivalent to BP in the way of updating parameters on any neural network, and it is thus a great breakthrough for the interdisciplinary research of neuroscience and deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge