Prediction and Sampling with Local Graph Transforms for Quasi-Lossless Light Field Compression

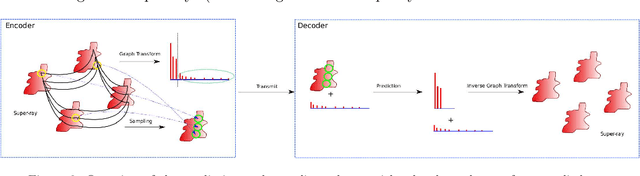
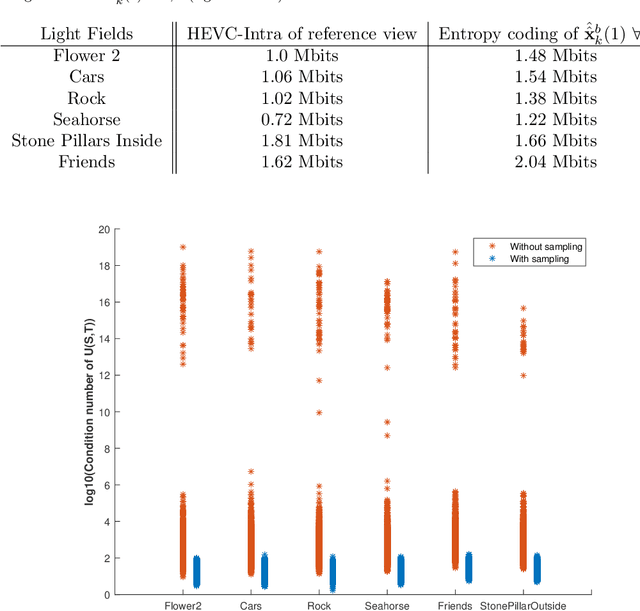
Graph-based transforms have been shown to be powerful tools in terms of image energy compaction. However, when the support increases to best capture signal dependencies, the computation of the basis functions becomes rapidly untractable. This problem is in particular compelling for high dimensional imaging data such as light fields. The use of local transforms with limited supports is a way to cope with this computational difficulty. Unfortunately, the locality of the support may not allow us to fully exploit long term signal dependencies present in both the spatial and angular dimensions in the case of light fields. This paper describes sampling and prediction schemes with local graph-based transforms enabling to efficiently compact the signal energy and exploit dependencies beyond the local graph support. The proposed approach is investigated and is shown to be very efficient in the context of spatio-angular transforms for quasi-lossless compression of light fields.