Polynomial Time Near-Time-Optimal Multi-Robot Path Planning in Three Dimensions with Applications to Large-Scale UAV Coordination
Paper and Code
Jul 06, 2022
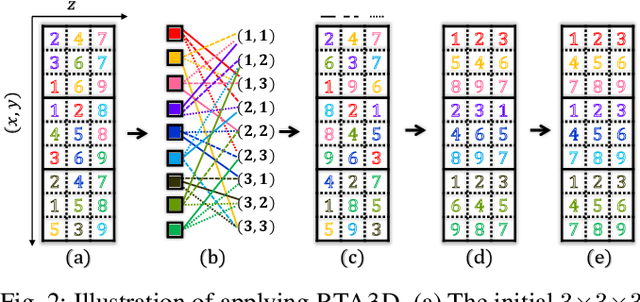


For enabling efficient, large-scale coordination of unmanned aerial vehicles (UAVs) under the labeled setting, in this work, we develop the first polynomial time algorithm for the reconfiguration of many moving bodies in three-dimensional spaces, with provable $1.x$ asymptotic makespan optimality guarantee under high robot density. More precisely, on an $m_1\times m_2 \times m_3$ grid, $m_1\ge m_2\ge m_3$, our method computes solutions for routing up to $\frac{m_1m_2m_3}{3}$ uniquely labeled robots with uniformly randomly distributed start and goal configurations within a makespan of $m_1 + 2m_2 +2m_3+o(m_1)$, with high probability. Because the makespan lower bound for such instances is $m_1 + m_2+m_3 - o(m_1)$, also with high probability, as $m_1 \to \infty$, $\frac{m_1+2m_2+2m_3}{m_1+m_2+m_3}$ optimality guarantee is achieved. $\frac{m_1+2m_2+2m_3}{m_1+m_2+m_3} \in (1, \frac{5}{3}]$, yielding $1.x$ optimality. In contrast, it is well-known that multi-robot path planning is NP-hard to optimally solve. In numerical evaluations, our method readily scales to support the motion planning of over $100,000$ robots in 3D while simultaneously achieving $1.x$ optimality. We demonstrate the application of our method in coordinating many quadcopters in both simulation and hardware experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge