Polygon Area Decomposition Using a Compactness Metric
Paper and Code
Oct 08, 2021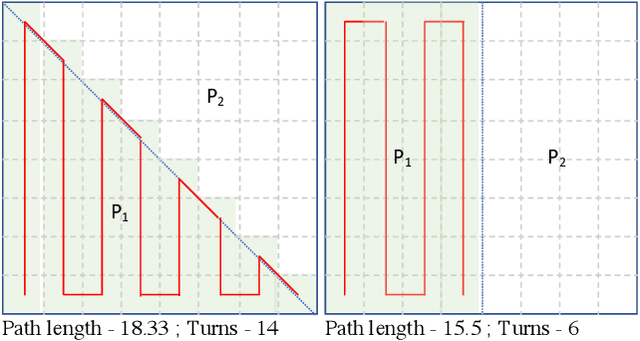
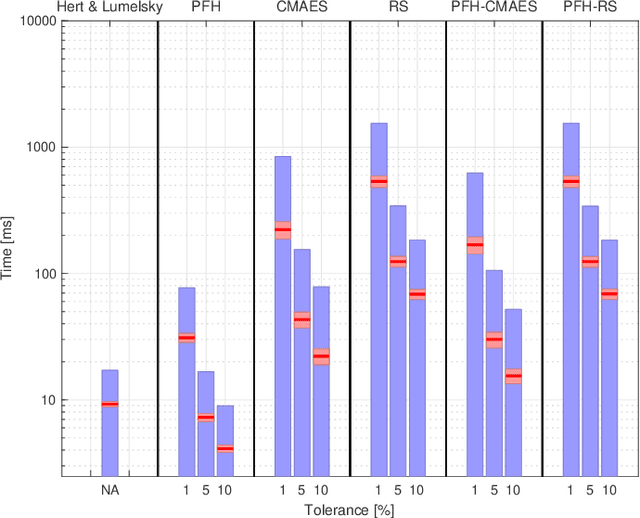
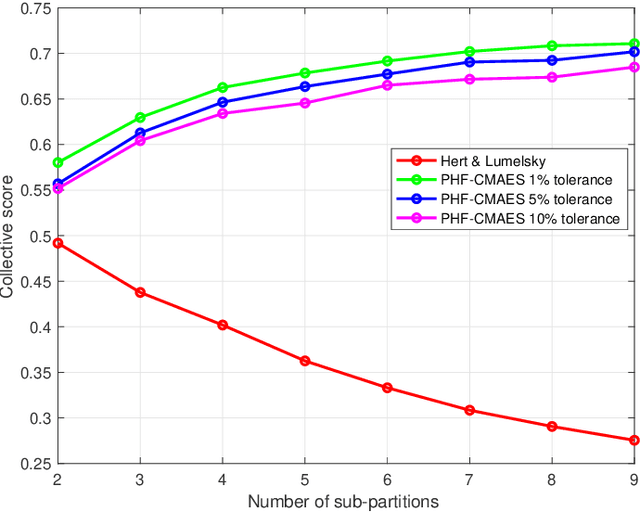
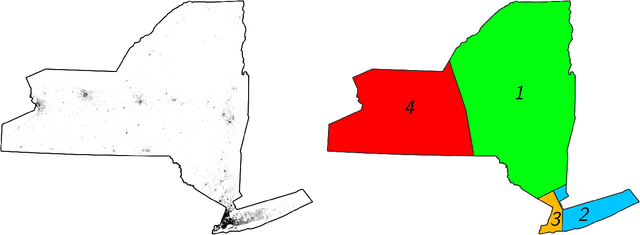
In this paper, we consider the problem of partitioning a polygon into a set of connected disjoint sub-polygons, each of which covers an area of a specific size. The work is motivated by terrain covering applications in robotics, where the goal is to find a set of efficient plans for a team of heterogeneous robots to cover a given area. Within this application, solving a polygon partitioning problem is an essential stepping stone. Unlike previous work, the problem formulation proposed in this paper also considers a compactness metric of the generated sub-polygons, in addition to the area size constraints. Maximizing the compactness of sub-polygons directly influences the optimality of any generated motion plans. Consequently, this increases the efficiency with which robotic tasks can be performed within each sub-region. The proposed problem representation is based on grid cell decomposition and a potential field model that allows for the use of standard optimization techniques. A new algorithm, the AreaDecompose algorithm, is proposed to solve this problem. The algorithm includes a number of existing and new optimization techniques combined with two post-processing methods. The approach has been evaluated on a set of randomly generated polygons which are then divided using different criteria and the results have been compared with a state-of-the-art algorithm. Results show that the proposed algorithm can efficiently divide polygon regions maximizing compactness of the resulting partitions, where the sub-polygon regions are on average up to 73% more compact in comparison to existing techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge