PMSSC: Parallelizable Multi-Subset based Self-Expressive Model for Subspace Clustering

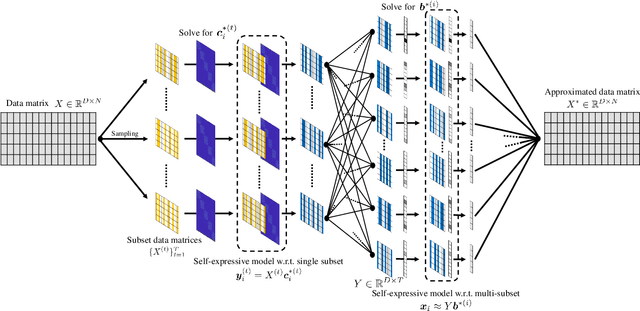
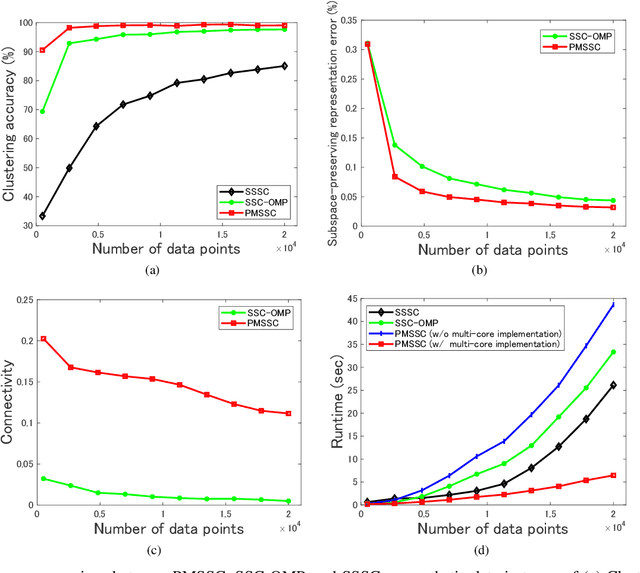
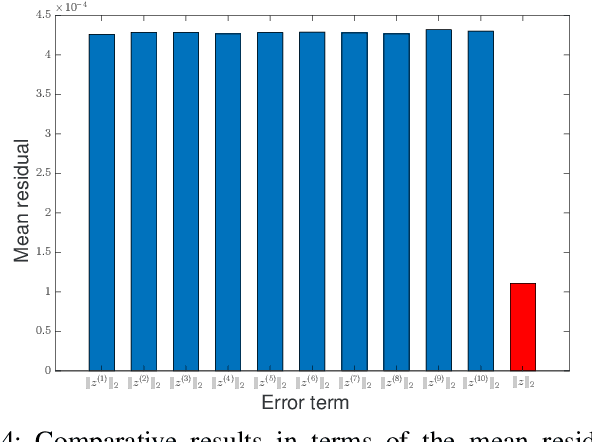
Subspace clustering methods embrace a self-expressive model that represents each data point as a linear combination of other data points in the dataset are powerful unsupervised learning techniques. However, when dealing with large-scale datasets, the representation of each data point by referring to all data points as a dictionary suffers from high computational complexity. To alleviate this issue, we introduce a parallelizable multi-subset based self-expressive model (PMS) which represents each data point by combing multiple subsets, with each consisting of only a small percentage of samples. The adoption of PMS in subspace clustering (PMSSC) leads to computational advantages because each optimization problem decomposed into each subset is small, and can be solved efficiently in parallel. Besides, PMSSC is able to combine multiple self-expressive coefficient vectors obtained from subsets, which contributes to the improvement of self-expressiveness. Extensive experiments on synthetic data and real-world datasets show the efficiency and effectiveness of our approach against competitive methods.