PINSAT: Parallelized Interleaving of Graph Search and Trajectory Optimization for Kinodynamic Motion Planning

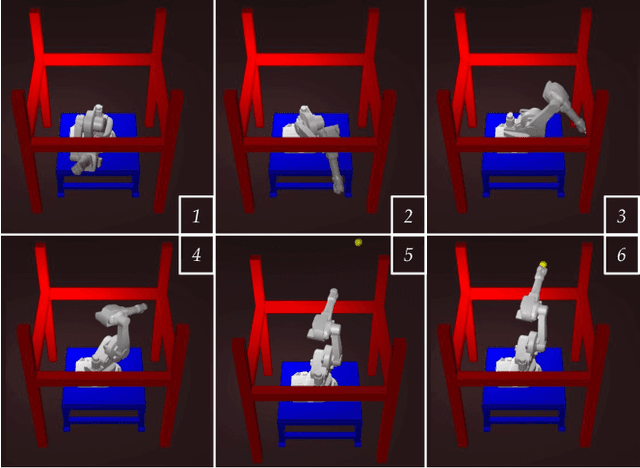
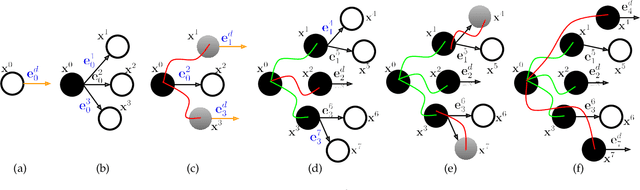
Trajectory optimization is a widely used technique in robot motion planning for letting the dynamics and constraints on the system shape and synthesize complex behaviors. Several previous works have shown its benefits in high-dimensional continuous state spaces and under differential constraints. However, long time horizons and planning around obstacles in non-convex spaces pose challenges in guaranteeing convergence or finding optimal solutions. As a result, discrete graph search planners and sampling-based planers are preferred when facing obstacle-cluttered environments. A recently developed algorithm called INSAT effectively combines graph search in the low-dimensional subspace and trajectory optimization in the full-dimensional space for global kinodynamic planning over long horizons. Although INSAT successfully reasoned about and solved complex planning problems, the numerous expensive calls to an optimizer resulted in large planning times, thereby limiting its practical use. Inspired by the recent work on edge-based parallel graph search, we present PINSAT, which introduces systematic parallelization in INSAT to achieve lower planning times and higher success rates, while maintaining significantly lower costs over relevant baselines. We demonstrate PINSAT by evaluating it on 6 DoF kinodynamic manipulation planning with obstacles.