Piecewise Flat Embedding for Image Segmentation
Paper and Code
May 20, 2018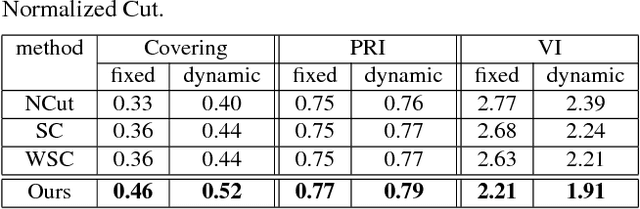

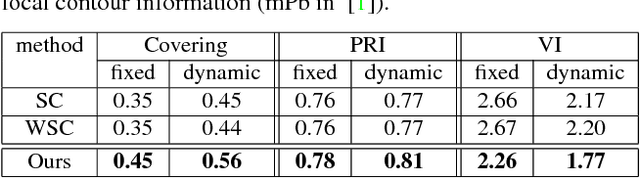
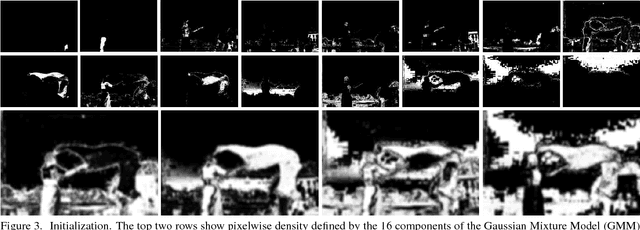
We introduce a new multi-dimensional nonlinear embedding -- Piecewise Flat Embedding (PFE) -- for image segmentation. Based on the theory of sparse signal recovery, piecewise flat embedding with diverse channels attempts to recover a piecewise constant image representation with sparse region boundaries and sparse cluster value scattering. The resultant piecewise flat embedding exhibits interesting properties such as suppressing slowly varying signals, and offers an image representation with higher region identifiability which is desirable for image segmentation or high-level semantic analysis tasks. We formulate our embedding as a variant of the Laplacian Eigenmap embedding with an $L_{1,p} (0<p\leq1)$ regularization term to promote sparse solutions. First, we devise a two-stage numerical algorithm based on Bregman iterations to compute $L_{1,1}$-regularized piecewise flat embeddings. We further generalize this algorithm through iterative reweighting to solve the general $L_{1,p}$-regularized problem. To demonstrate its efficacy, we integrate PFE into two existing image segmentation frameworks, segmentation based on clustering and hierarchical segmentation based on contour detection. Experiments on four major benchmark datasets, BSDS500, MSRC, Stanford Background Dataset, and PASCAL Context, show that segmentation algorithms incorporating our embedding achieve significantly improved results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge