Photometric Stereo by Hemispherical Metric Embedding
Paper and Code
Jun 25, 2017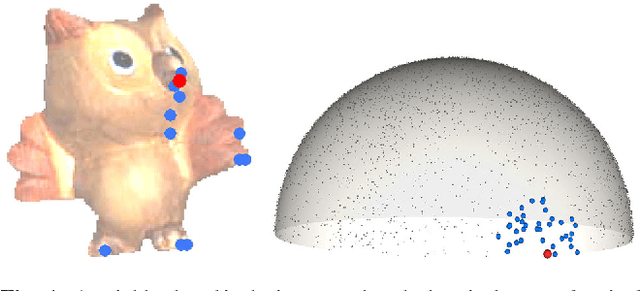
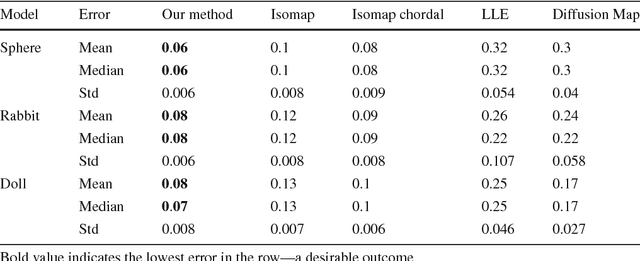
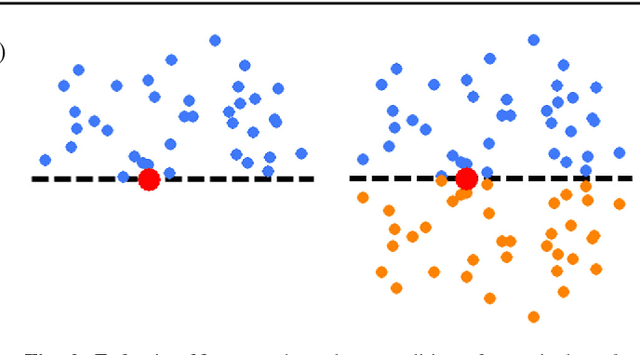
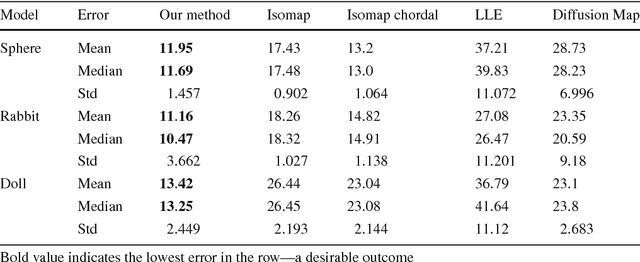
Photometric Stereo methods seek to reconstruct the 3d shape of an object from motionless images obtained with varying illumination. Most existing methods solve a restricted problem where the physical reflectance model, such as Lambertian reflectance, is known in advance. In contrast, we do not restrict ourselves to a specific reflectance model. Instead, we offer a method that works on a wide variety of reflectances. Our approach uses a simple yet uncommonly used property of the problem - the sought after normals are points on a unit hemisphere. We present a novel embedding method that maps pixels to normals on the unit hemisphere. Our experiments demonstrate that this approach outperforms existing manifold learning methods for the task of hemisphere embedding. We further show successful reconstructions of objects from a wide variety of reflectances including smooth, rough, diffuse and specular surfaces, even in the presence of significant attached shadows. Finally, we empirically prove that under these challenging settings we obtain more accurate shape reconstructions than existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge