Persistent Homology Captures the Generalization of Neural Networks Without A Validation Set
Paper and Code
May 31, 2021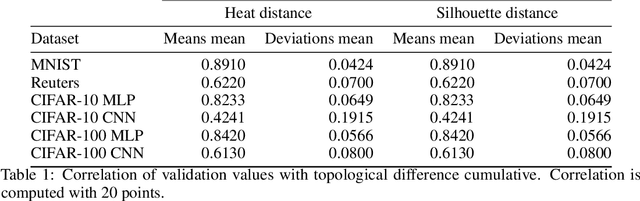
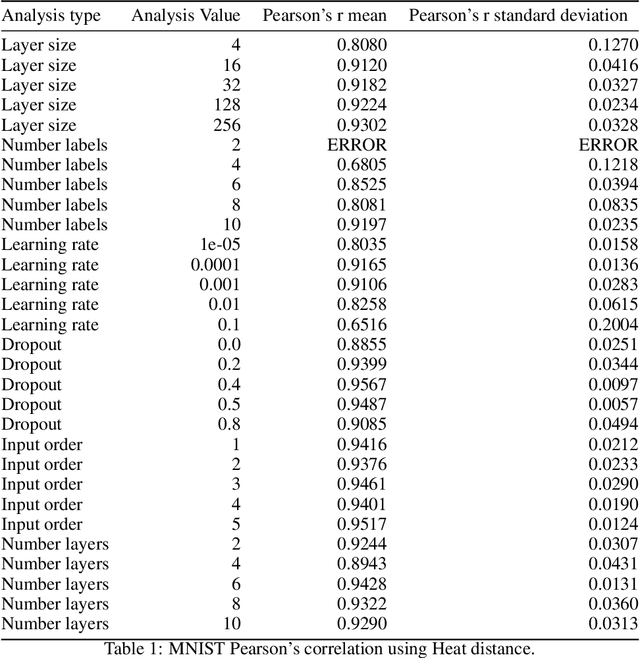

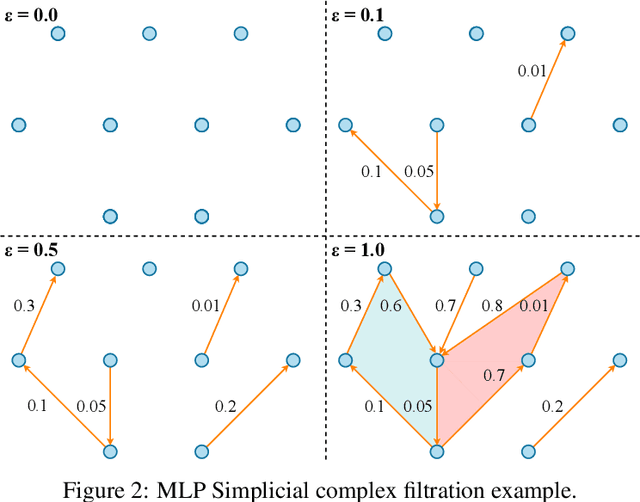
The training of neural networks is usually monitored with a validation (holdout) set to estimate the generalization of the model. This is done instead of measuring intrinsic properties of the model to determine whether it is learning appropriately. In this work, we suggest studying the training of neural networks with Algebraic Topology, specifically Persistent Homology (PH). Using simplicial complex representations of neural networks, we study the PH diagram distance evolution on the neural network learning process with different architectures and several datasets. Results show that the PH diagram distance between consecutive neural network states correlates with the validation accuracy, implying that the generalization error of a neural network could be intrinsically estimated without any holdout set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge