Performance Bounds for Near-Field Localization with Widely-Spaced Multi-Subarray mmWave/THz MIMO

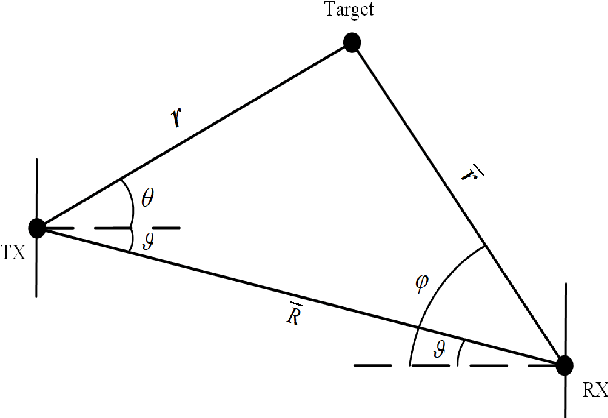
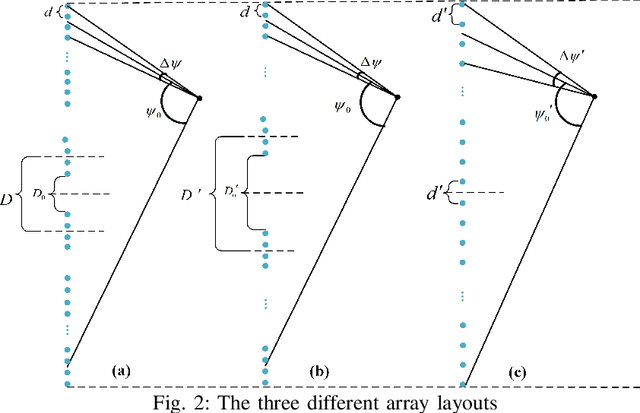
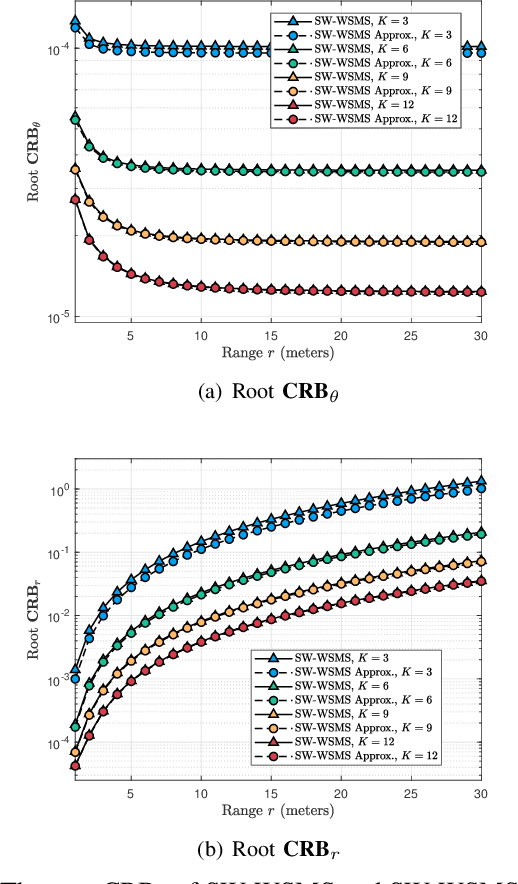
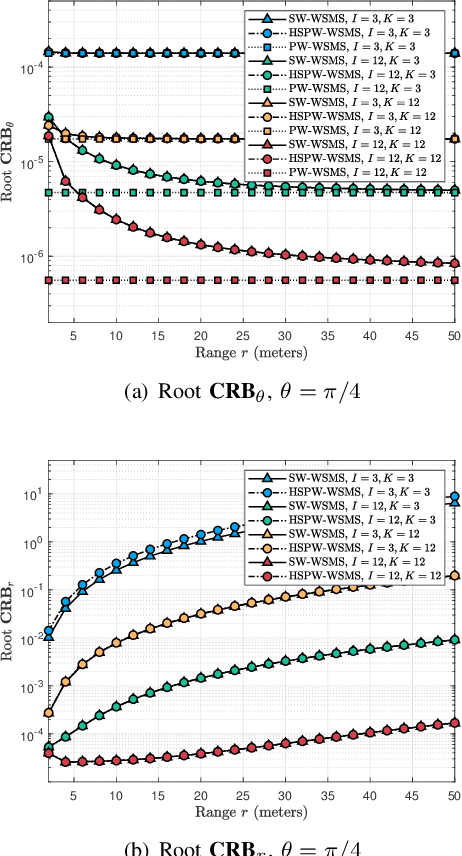
This paper investigates the potential of near-field localization using widely-spaced multi-subarrays (WSMSs) and analyzing the corresponding angle and range Cram\'er-Rao bounds (CRBs). By employing the Riemann sum, closed-form CRB expressions are derived for the spherical wavefront-based WSMS (SW-WSMS). We find that the CRBs can be characterized by the angular span formed by the line connecting the array's two ends to the target, and the different WSMSs with same angular spans but different number of subarrays have identical normalized CRBs. We provide a theoretical proof that, in certain scenarios, the CRB of WSMSs is smaller than that of uniform arrays. We further yield the closed-form CRBs for the hybrid spherical and planar wavefront-based WSMS (HSPW-WSMS), and its components can be seen as decompositions of the parameters from the CRBs for the SW-WSMS. Simulations are conducted to validate the accuracy of the derived closed-form CRBs and provide further insights into various system characteristics. Basically, this paper underscores the high resolution of utilizing WSMS for localization, reinforces the validity of adopting the HSPW assumption, and, considering its applications in communications, indicates a promising outlook for integrated sensing and communications based on HSPW-WSMSs.