Performance Analysis of Multiple-Antenna Ambient Backscatter Systems at Finite Blocklengths
Paper and Code
Jan 25, 2022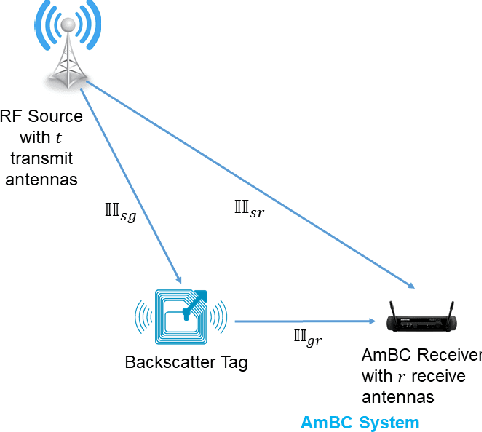
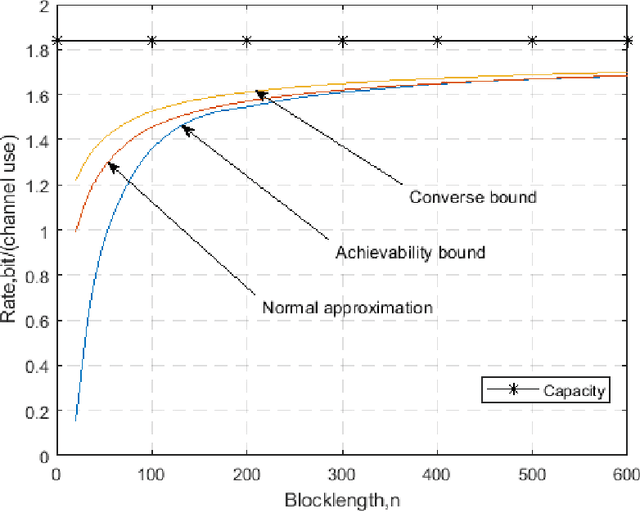
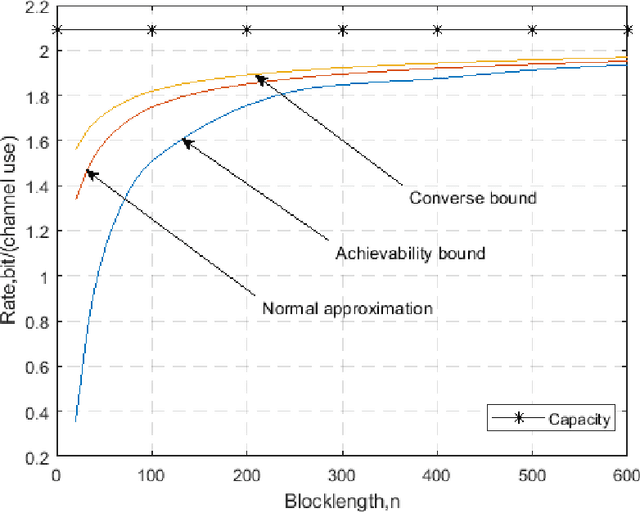
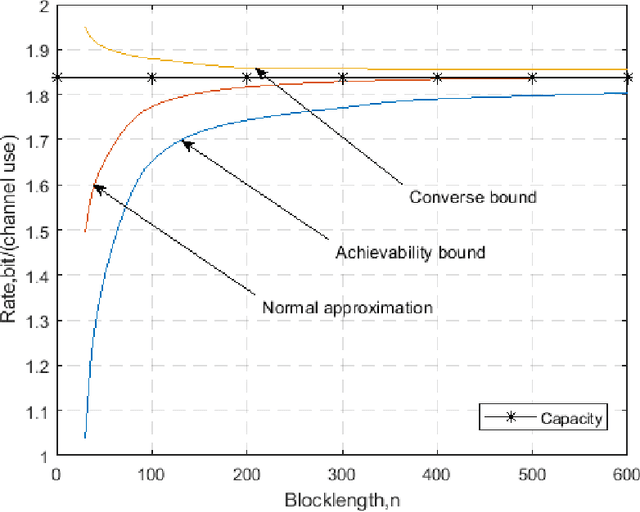
This paper analyzes the maximal achievable rate for a given blocklength and error probability over a multiple-antenna ambient backscatter channel with perfect channel state information at the receiver. The result consists of a finite blocklength channel coding achievability bound and a converse bound based on the Neyman-Pearson test and the normal approximation based on the Berry- Esseen Theorem. Numerical evaluation of these bounds shows fast convergence to the channel capacity as the blocklength increases and also proves that the channel dispersion is an accurate measure of the backoff from capacity due to finite blocklength.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge