Perfect Alignment May be Poisonous to Graph Contrastive Learning

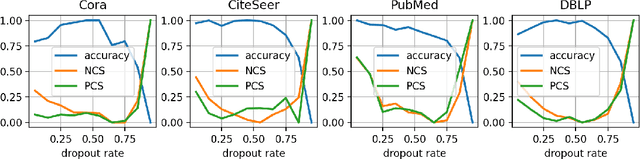
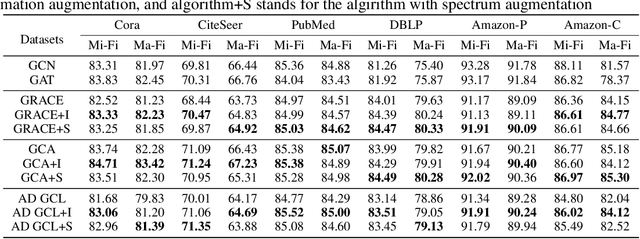
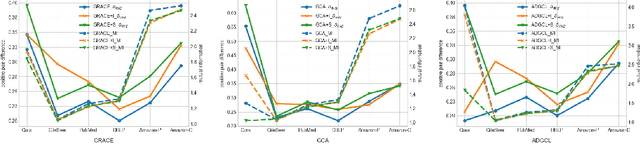
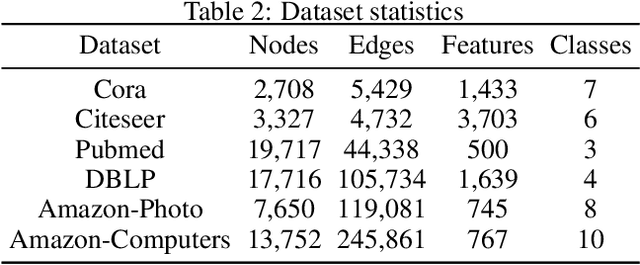
Graph Contrastive Learning (GCL) aims to learn node representations by aligning positive pairs and separating negative ones. However, limited research has been conducted on the inner law behind specific augmentations used in graph-based learning. What kind of augmentation will help downstream performance, how does contrastive learning actually influence downstream tasks, and why the magnitude of augmentation matters? This paper seeks to address these questions by establishing a connection between augmentation and downstream performance, as well as by investigating the generalization of contrastive learning. Our findings reveal that GCL contributes to downstream tasks mainly by separating different classes rather than gathering nodes of the same class. So perfect alignment and augmentation overlap which draw all intra-class samples the same can not explain the success of contrastive learning. Then in order to comprehend how augmentation aids the contrastive learning process, we conduct further investigations into its generalization, finding that perfect alignment that draw positive pair the same could help contrastive loss but is poisonous to generalization, on the contrary, imperfect alignment enhances the model's generalization ability. We analyse the result by information theory and graph spectrum theory respectively, and propose two simple but effective methods to verify the theories. The two methods could be easily applied to various GCL algorithms and extensive experiments are conducted to prove its effectiveness.