PCE-PINNs: Physics-Informed Neural Networks for Uncertainty Propagation in Ocean Modeling
Paper and Code
May 05, 2021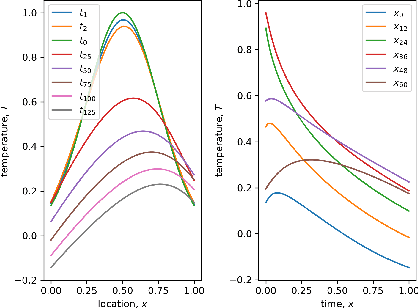
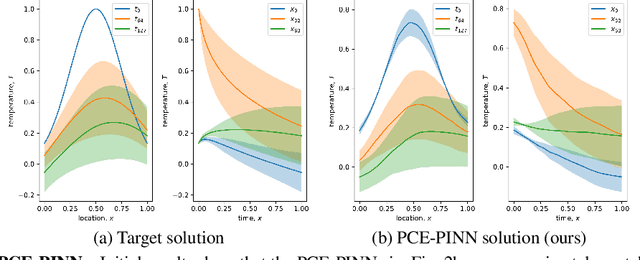
Climate models project an uncertainty range of possible warming scenarios from 1.5 to 5 degree Celsius global temperature increase until 2100, according to the CMIP6 model ensemble. Climate risk management and infrastructure adaptation requires the accurate quantification of the uncertainties at the local level. Ensembles of high-resolution climate models could accurately quantify the uncertainties, but most physics-based climate models are computationally too expensive to run as ensemble. Recent works in physics-informed neural networks (PINNs) have combined deep learning and the physical sciences to learn up to 15k faster copies of climate submodels. However, the application of PINNs in climate modeling has so far been mostly limited to deterministic models. We leverage a novel method that combines polynomial chaos expansion (PCE), a classic technique for uncertainty propagation, with PINNs. The PCE-PINNs learn a fast surrogate model that is demonstrated for uncertainty propagation of known parameter uncertainties. We showcase the effectiveness in ocean modeling by using the local advection-diffusion equation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge