Path Planning in Dynamic Environments with Adaptive Dimensionality
Paper and Code
May 22, 2016
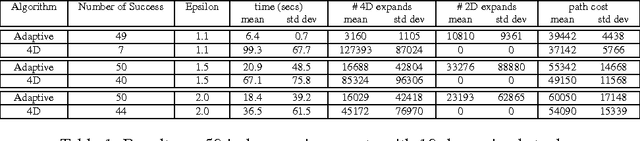

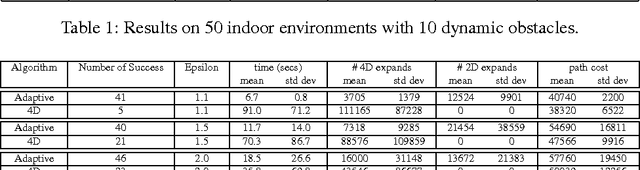
Path planning in the presence of dynamic obstacles is a challenging problem due to the added time dimension in search space. In approaches that ignore the time dimension and treat dynamic obstacles as static, frequent re-planning is unavoidable as the obstacles move, and their solutions are generally sub-optimal and can be incomplete. To achieve both optimality and completeness, it is necessary to consider the time dimension during planning. The notion of adaptive dimensionality has been successfully used in high-dimensional motion planning such as manipulation of robot arms, but has not been used in the context of path planning in dynamic environments. In this paper, we apply the idea of adaptive dimensionality to speed up path planning in dynamic environments for a robot with no assumptions on its dynamic model. Specifically, our approach considers the time dimension only in those regions of the environment where a potential collision may occur, and plans in a low-dimensional state-space elsewhere. We show that our approach is complete and is guaranteed to find a solution, if one exists, within a cost sub-optimality bound. We experimentally validate our method on the problem of 3D vehicle navigation (x, y, heading) in dynamic environments. Our results show that the presented approach achieves substantial speedups in planning time over 4D heuristic-based A*, especially when the resulting plan deviates significantly from the one suggested by the heuristic.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge