Pareto Actor-Critic for Equilibrium Selection in Multi-Agent Reinforcement Learning

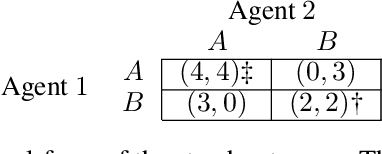
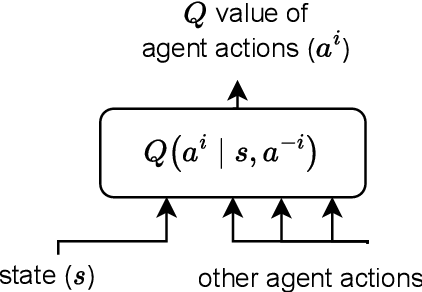
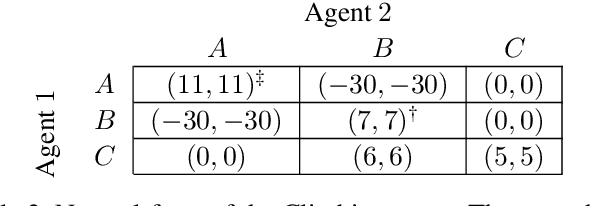
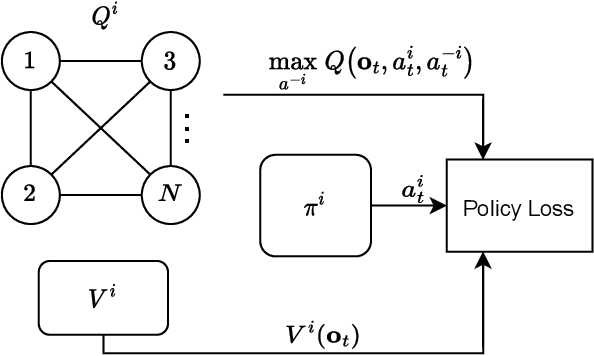
Equilibrium selection in multi-agent games refers to the problem of selecting a Pareto-optimal equilibrium. It has been shown that many state-of-the-art multi-agent reinforcement learning (MARL) algorithms are prone to converging to Pareto-dominated equilibria due to the uncertainty each agent has about the policy of the other agents during training. To address suboptimal equilibrium selection, we propose Pareto-AC (PAC), an actor-critic algorithm that utilises a simple principle of no-conflict games (a superset of cooperative games with identical rewards): each agent can assume the others will choose actions that will lead to a Pareto-optimal equilibrium. We evaluate PAC in a diverse set of multi-agent games and show that it converges to higher episodic returns compared to alternative MARL algorithms, as well as successfully converging to a Pareto-optimal equilibrium in a range of matrix games. Finally, we propose a graph neural network extension which is shown to efficiently scale in games with up to 15 agents.