PAN: Path Integral Based Convolution for Deep Graph Neural Networks
Paper and Code
Apr 24, 2019
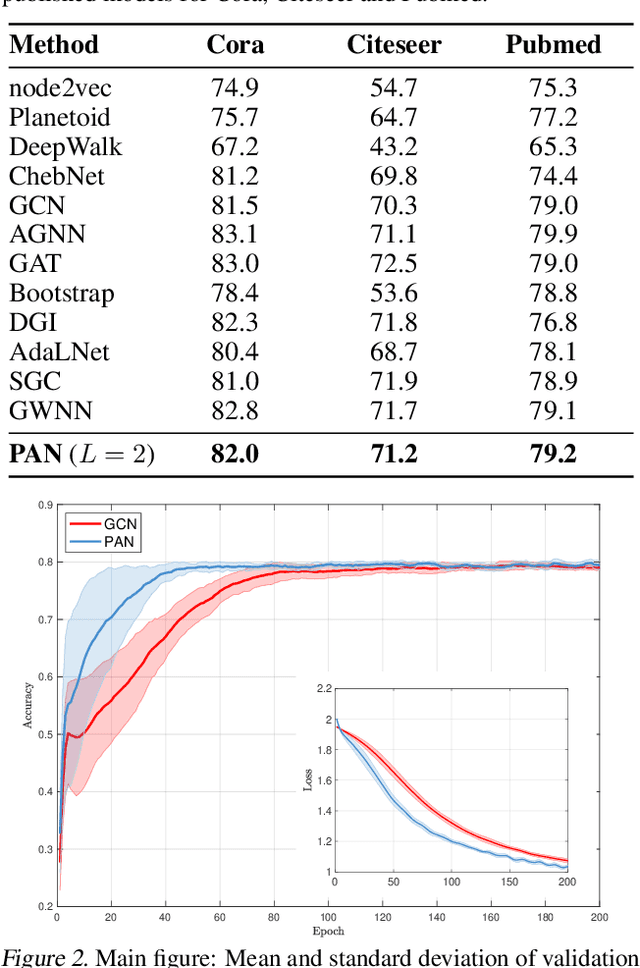
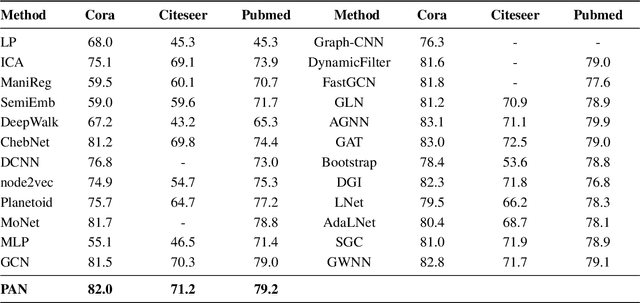
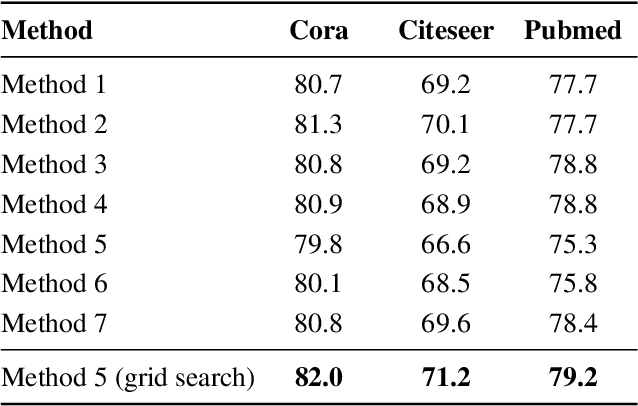
Convolution operations designed for graph-structured data usually utilize the graph Laplacian, which can be seen as message passing between the adjacent neighbors through a generic random walk. In this paper, we propose PAN, a new graph convolution framework that involves every path linking the message sender and receiver with learnable weights depending on the path length, which corresponds to the maximal entropy random walk. PAN generalizes the graph Laplacian to a new transition matrix we call \emph{maximal entropy transition} (MET) matrix derived from a path integral formalism. Most previous graph convolutional network architectures can be adapted to our framework, and many variations and derivatives based on the path integral idea can be developed. Experimental results show that the path integral based graph neural networks have great learnability and fast convergence rate, and achieve state-of-the-art performance on benchmark tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge