PAC-Bayesian Domain Adaptation Bounds for Multiclass Learners

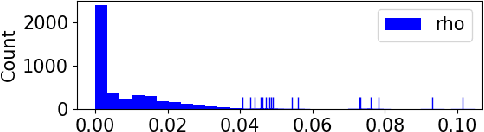
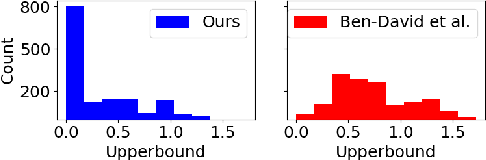
Multiclass neural networks are a common tool in modern unsupervised domain adaptation, yet an appropriate theoretical description for their non-uniform sample complexity is lacking in the adaptation literature. To fill this gap, we propose the first PAC-Bayesian adaptation bounds for multiclass learners. We facilitate practical use of our bounds by also proposing the first approximation techniques for the multiclass distribution divergences we consider. For divergences dependent on a Gibbs predictor, we propose additional PAC-Bayesian adaptation bounds which remove the need for inefficient Monte-Carlo estimation. Empirically, we test the efficacy of our proposed approximation techniques as well as some novel design-concepts which we include in our bounds. Finally, we apply our bounds to analyze a common adaptation algorithm that uses neural networks.