PAC-Bayesian Contrastive Unsupervised Representation Learning

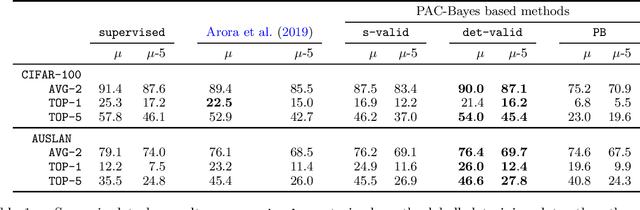
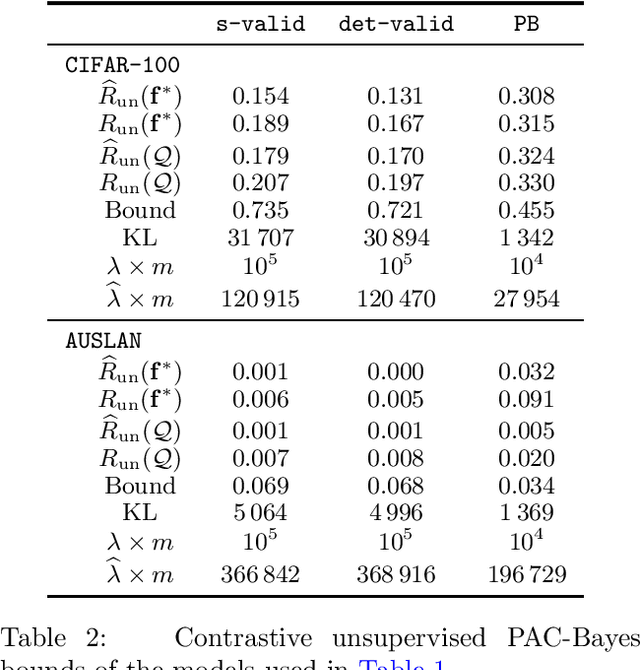
Contrastive unsupervised representation learning (CURL) is the state-of-the-art technique to learn representations (as a set of features) from unlabelled data. While CURL has collected several empirical successes recently, theoretical understanding of its performance was still missing. In a recent work, Arora et al. (2019) provide the first generalisation bounds for CURL, relying on a Rademacher complexity. We extend their framework to the flexible PAC-Bayes setting, allowing to deal with the non-iid setting. We present PAC-Bayesian generalisation bounds for CURL, which are then used to derive a new representation learning algorithm. Numerical experiments on real-life datasets illustrate that our algorithm achieves competitive accuracy, and yields generalisation bounds with non-vacuous values.