P-MCGS: Parallel Monte Carlo Acyclic Graph Search
Paper and Code
Oct 28, 2018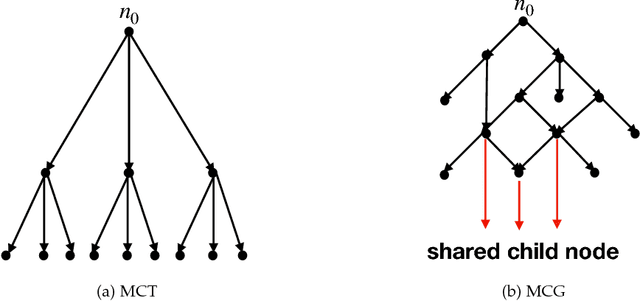
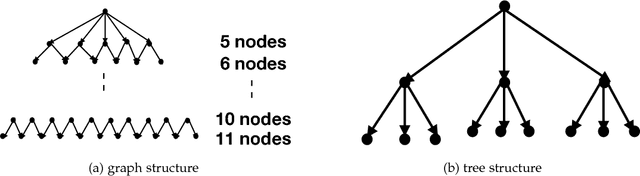
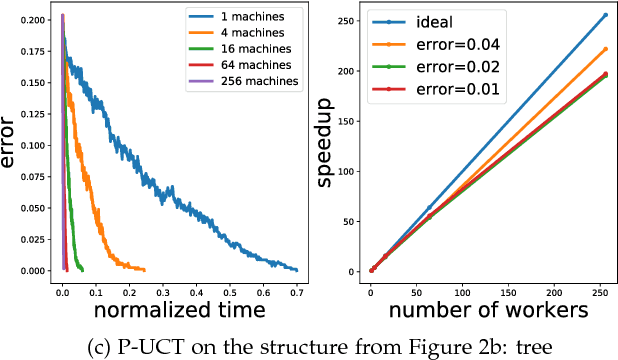
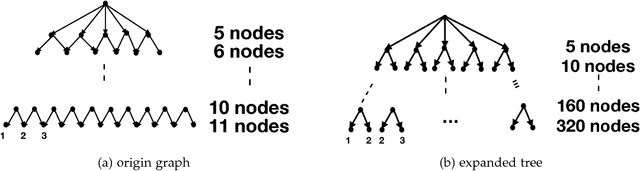
Recently, there have been great interests in Monte Carlo Tree Search (MCTS) in AI research. Although the sequential version of MCTS has been studied widely, its parallel counterpart still lacks systematic study. This leads us to the following questions: \emph{how to design efficient parallel MCTS (or more general cases) algorithms with rigorous theoretical guarantee? Is it possible to achieve linear speedup?} In this paper, we consider the search problem on a more general acyclic one-root graph (namely, Monte Carlo Graph Search (MCGS)), which generalizes MCTS. We develop a parallel algorithm (P-MCGS) to assign multiple workers to investigate appropriate leaf nodes simultaneously. Our analysis shows that P-MCGS algorithm achieves linear speedup and that the sample complexity is comparable to its sequential counterpart.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge