Optimization Strategies in Multi-Task Learning: Averaged or Independent Losses?
Paper and Code
Oct 04, 2021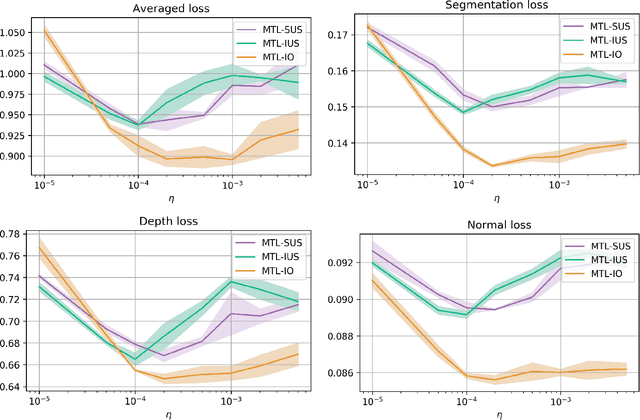
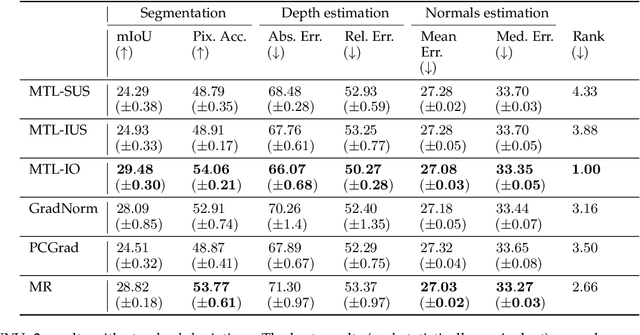
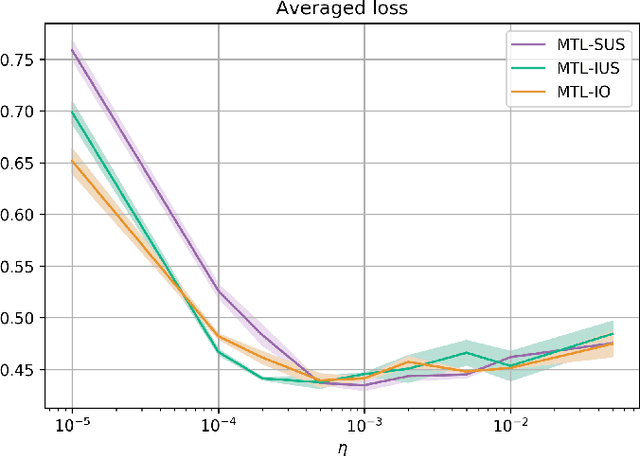
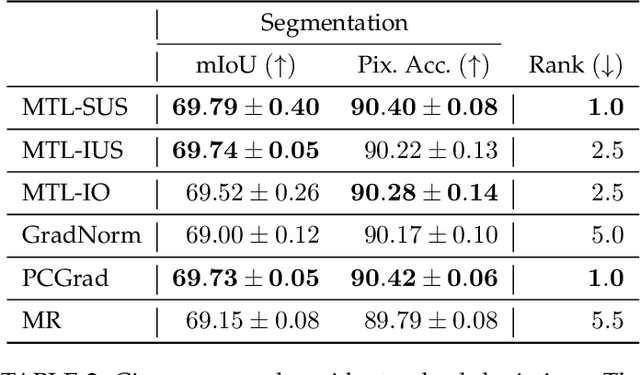
In Multi-Task Learning (MTL), it is a common practice to train multi-task networks by optimizing an objective function, which is a weighted average of the task-specific objective functions. Although the computational advantages of this strategy are clear, the complexity of the resulting loss landscape has not been studied in the literature. Arguably, its optimization may be more difficult than a separate optimization of the constituting task-specific objectives. In this work, we investigate the benefits of such an alternative, by alternating independent gradient descent steps on the different task-specific objective functions and we formulate a novel way to combine this approach with state-of-the-art optimizers. As the separation of task-specific objectives comes at the cost of increased computational time, we propose a random task grouping as a trade-off between better optimization and computational efficiency. Experimental results over three well-known visual MTL datasets show better overall absolute performance on losses and standard metrics compared to an averaged objective function and other state-of-the-art MTL methods. In particular, our method shows the most benefits when dealing with tasks of different nature and it enables a wider exploration of the shared parameter space. We also show that our random grouping strategy allows to trade-off between these benefits and computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge