Optimization Insights into Deep Diagonal Linear Networks
Paper and Code
Dec 21, 2024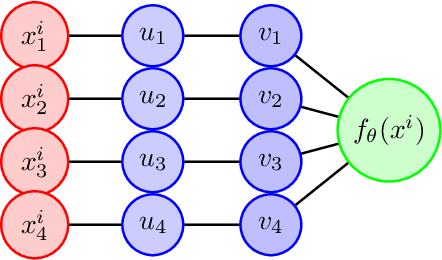
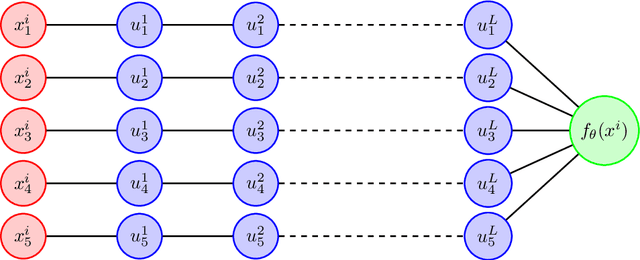
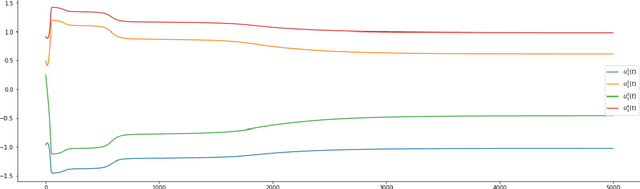
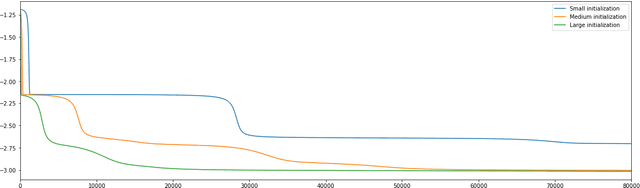
Overparameterized models trained with (stochastic) gradient descent are ubiquitous in modern machine learning. These large models achieve unprecedented performance on test data, but their theoretical understanding is still limited. In this paper, we take a step towards filling this gap by adopting an optimization perspective. More precisely, we study the implicit regularization properties of the gradient flow "algorithm" for estimating the parameters of a deep diagonal neural network. Our main contribution is showing that this gradient flow induces a mirror flow dynamic on the model, meaning that it is biased towards a specific solution of the problem depending on the initialization of the network. Along the way, we prove several properties of the trajectory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge