Optimization-Induced Graph Implicit Nonlinear Diffusion
Paper and Code
Jun 29, 2022
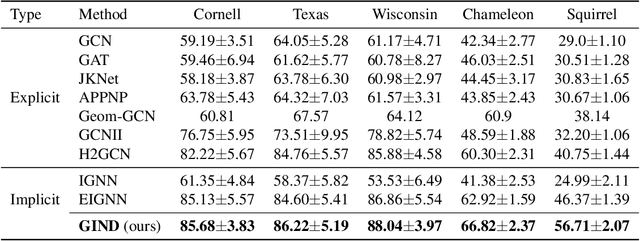
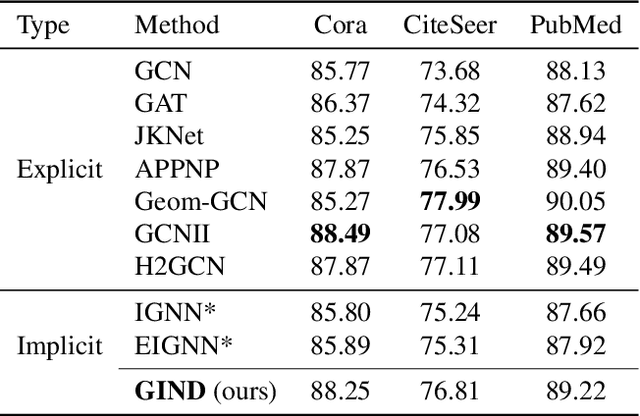
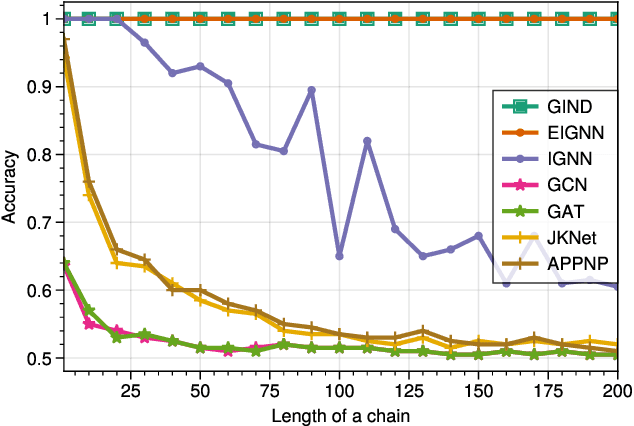
Due to the over-smoothing issue, most existing graph neural networks can only capture limited dependencies with their inherently finite aggregation layers. To overcome this limitation, we propose a new kind of graph convolution, called Graph Implicit Nonlinear Diffusion (GIND), which implicitly has access to infinite hops of neighbors while adaptively aggregating features with nonlinear diffusion to prevent over-smoothing. Notably, we show that the learned representation can be formalized as the minimizer of an explicit convex optimization objective. With this property, we can theoretically characterize the equilibrium of our GIND from an optimization perspective. More interestingly, we can induce new structural variants by modifying the corresponding optimization objective. To be specific, we can embed prior properties to the equilibrium, as well as introducing skip connections to promote training stability. Extensive experiments show that GIND is good at capturing long-range dependencies, and performs well on both homophilic and heterophilic graphs with nonlinear diffusion. Moreover, we show that the optimization-induced variants of our models can boost the performance and improve training stability and efficiency as well. As a result, our GIND obtains significant improvements on both node-level and graph-level tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge