Optimality of the Proper Gaussian Signal in Complex MIMO Wiretap Channels
Paper and Code
Sep 28, 2022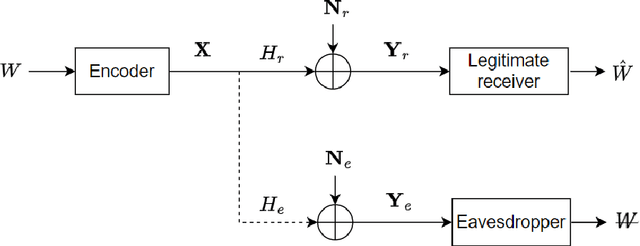
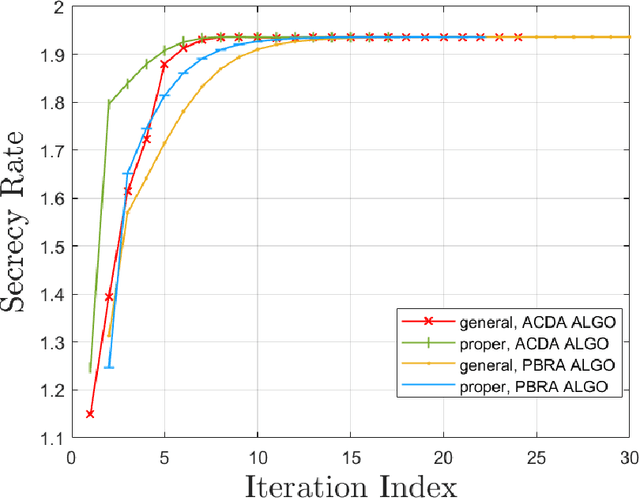
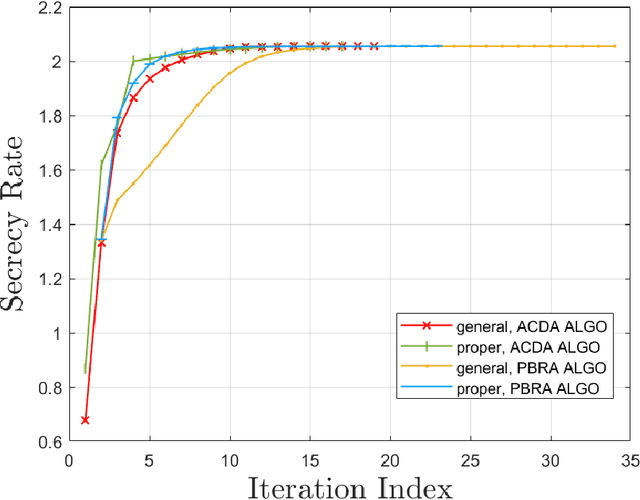
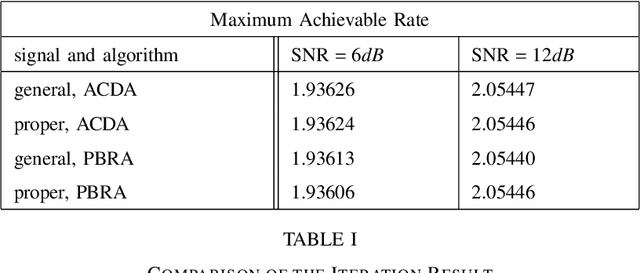
The multiple-input multiple-output (MIMO) wiretap channel (WTC), which has a transmitter, a legitimate user and an eavesdropper, is a classic model for studying information theoretic secrecy. In this paper, the fundamental problem for the complex WTC is whether the proper signal is optimal has yet to be given explicit proof, though previous work implicitly assumed the complex signal was proper. Thus, a determinant inequality is proposed to prove that the secrecy rate of a complex Gaussian signal with a fixed covariance matrix in a degraded complex WTC is maximized if and only if the signal is proper, i.e., the pseudo-covariance matrix is a zero matrix. Moreover, based on the result of the degraded complex WTC and the min-max reformulation of the secrecy capacity, the optimality of the proper signal in the general complex WTC is also revealed. The results of this research complement the current research on complex WTC. To be more specific, we have shown it is sufficient to focus on the proper signal when studying the secrecy capacity of the complex WTC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge