Optimal Model Averaging: Towards Personalized Collaborative Learning
Paper and Code
Oct 25, 2021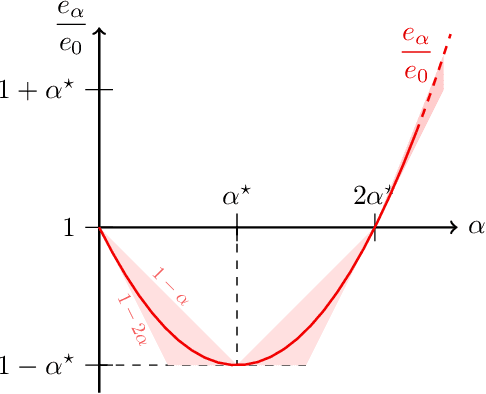
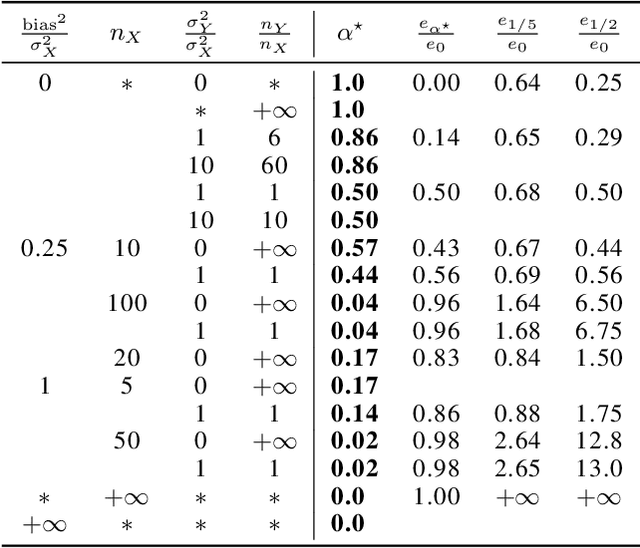
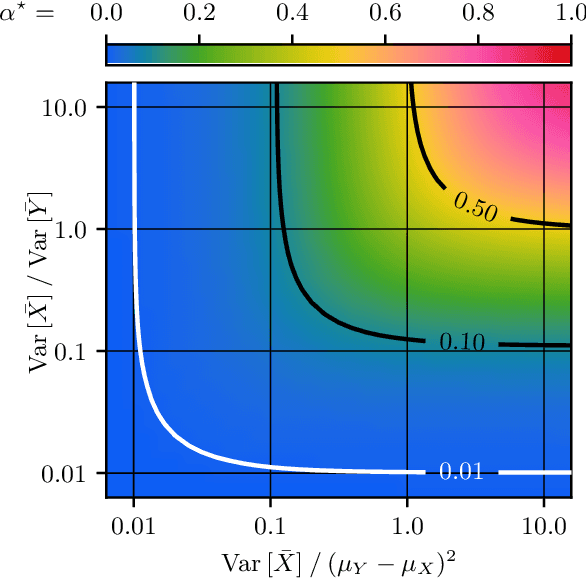
In federated learning, differences in the data or objectives between the participating nodes motivate approaches to train a personalized machine learning model for each node. One such approach is weighted averaging between a locally trained model and the global model. In this theoretical work, we study weighted model averaging for arbitrary scalar mean estimation problems under minimal assumptions on the distributions. In a variant of the bias-variance trade-off, we find that there is always some positive amount of model averaging that reduces the expected squared error compared to the local model, provided only that the local model has a non-zero variance. Further, we quantify the (possibly negative) benefit of weighted model averaging as a function of the weight used and the optimal weight. Taken together, this work formalizes an approach to quantify the value of personalization in collaborative learning and provides a framework for future research to test the findings in multivariate parameter estimation and under a range of assumptions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge