Optimal Gradient Compression for Distributed and Federated Learning
Paper and Code
Oct 07, 2020
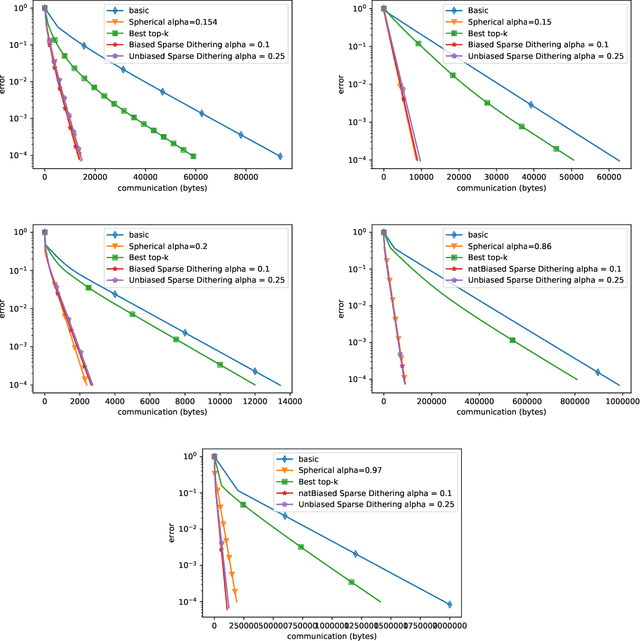
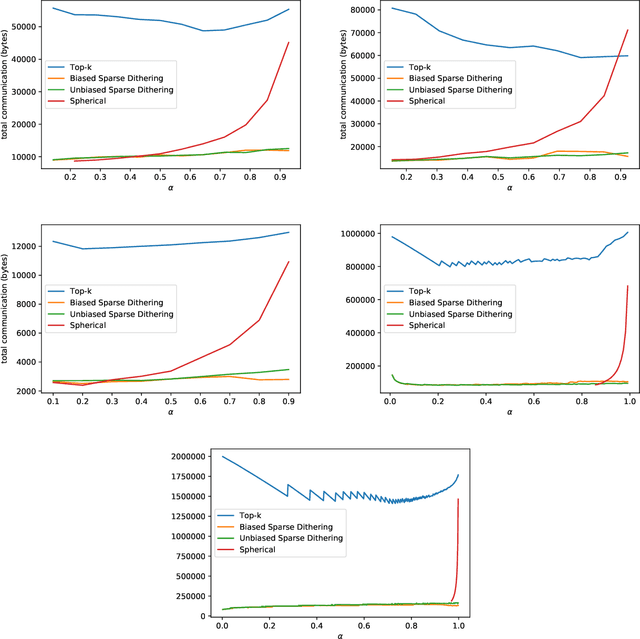

Communicating information, like gradient vectors, between computing nodes in distributed and federated learning is typically an unavoidable burden, resulting in scalability issues. Indeed, communication might be slow and costly. Recent advances in communication-efficient training algorithms have reduced this bottleneck by using compression techniques, in the form of sparsification, quantization, or low-rank approximation. Since compression is a lossy, or inexact, process, the iteration complexity is typically worsened; but the total communication complexity can improve significantly, possibly leading to large computation time savings. In this paper, we investigate the fundamental trade-off between the number of bits needed to encode compressed vectors and the compression error. We perform both worst-case and average-case analysis, providing tight lower bounds. In the worst-case analysis, we introduce an efficient compression operator, Sparse Dithering, which is very close to the lower bound. In the average-case analysis, we design a simple compression operator, Spherical Compression, which naturally achieves the lower bound. Thus, our new compression schemes significantly outperform the state of the art. We conduct numerical experiments to illustrate this improvement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge