Optimal estimation of Gaussian DAG models
Paper and Code
Jan 25, 2022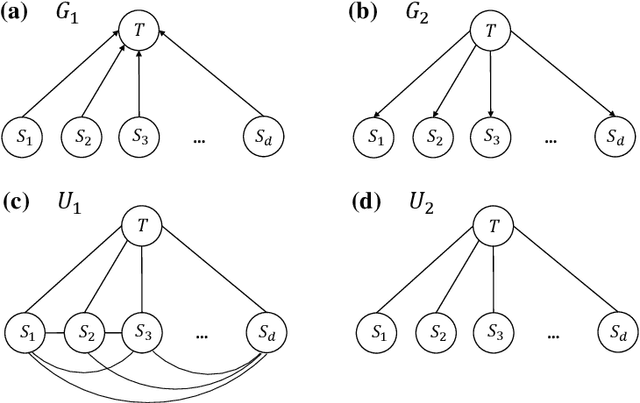
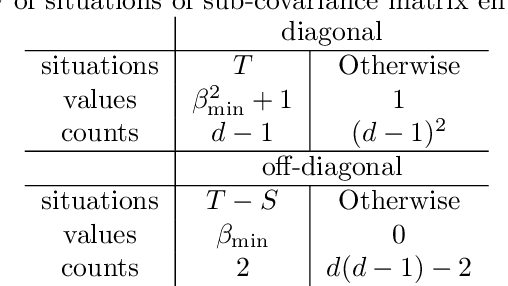

We study the optimal sample complexity of learning a Gaussian directed acyclic graph (DAG) from observational data. Our main result establishes the minimax optimal sample complexity for learning the structure of a linear Gaussian DAG model with equal variances to be $n\asymp q\log(d/q)$, where $q$ is the maximum number of parents and $d$ is the number of nodes. We further make comparisons with the classical problem of learning (undirected) Gaussian graphical models, showing that under the equal variance assumption, these two problems share the same optimal sample complexity. In other words, at least for Gaussian models with equal error variances, learning a directed graphical model is not more difficult than learning an undirected graphical model. Our results also extend to more general identification assumptions as well as subgaussian errors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge