Optimal Correlated Equilibria in General-Sum Extensive-Form Games: Fixed-Parameter Algorithms, Hardness, and Two-Sided Column-Generation

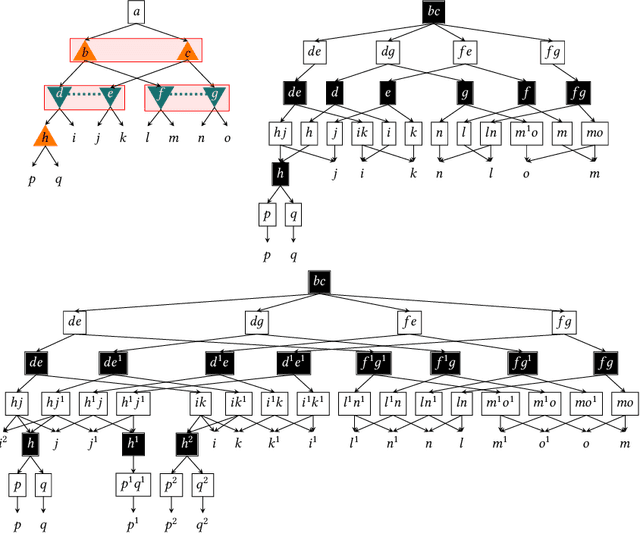
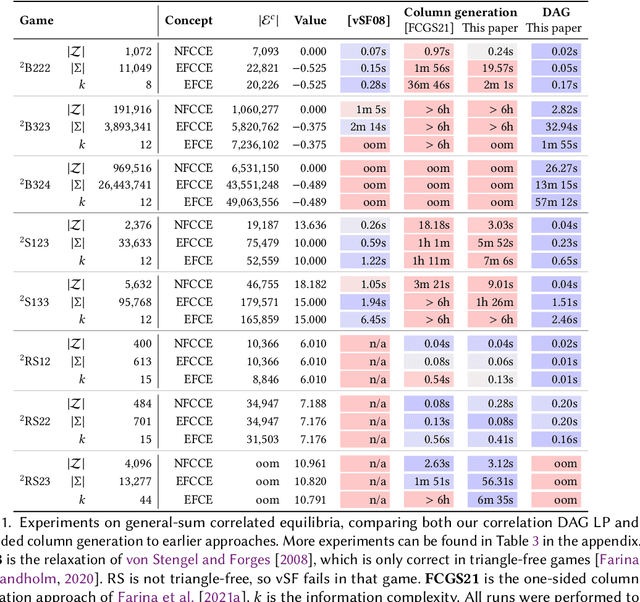
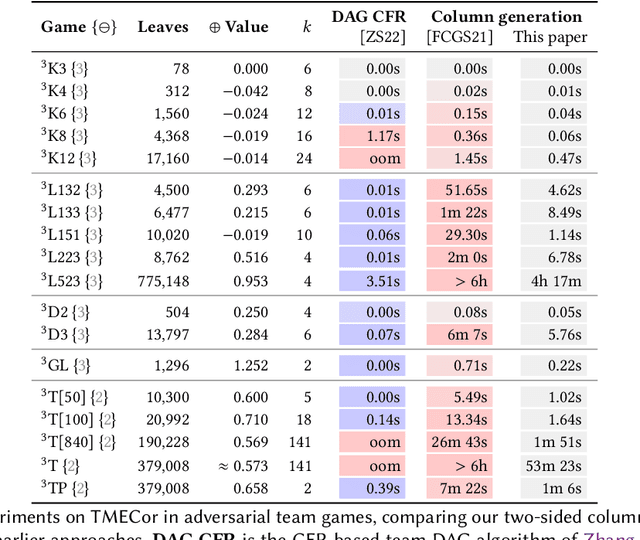
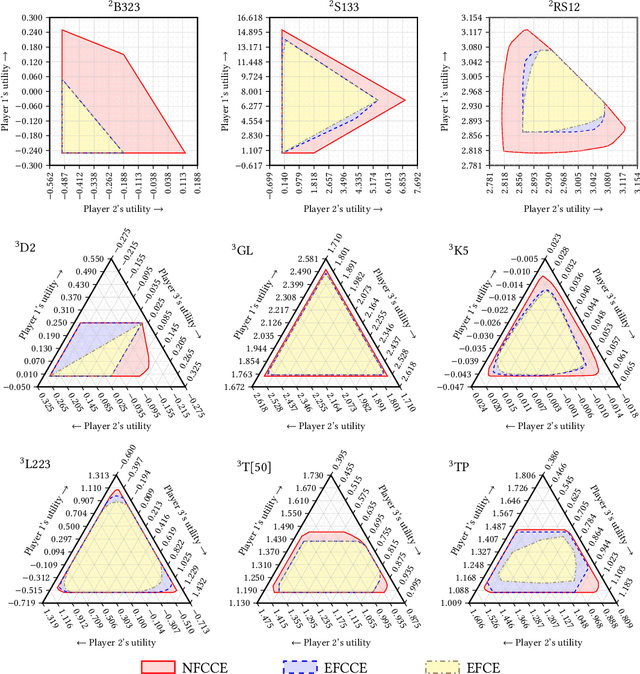
We study the problem of finding optimal correlated equilibria of various sorts: normal-form coarse correlated equilibrium (NFCCE), extensive-form coarse correlated equilibrium (EFCCE), and extensive-form correlated equilibrium (EFCE). This is NP-hard in the general case and has been studied in special cases, most notably triangle-free games, which include all two-player games with public chance moves. However, the general case is not well understood, and algorithms usually scale poorly. First, we introduce the correlation DAG, a representation of the space of correlated strategies whose size is dependent on the specific solution concept. It extends the team belief DAG of Zhang et al. to general-sum games. For each of the three solution concepts, its size depends exponentially only on a parameter related to the game's information structure. We also prove a fundamental complexity gap: while our size bounds for NFCCE are similar to those achieved in the case of team games by Zhang et al., this is impossible to achieve for the other two concepts under standard complexity assumptions. Second, we propose a two-sided column generation approach to compute optimal correlated strategies. Our algorithm improves upon the one-sided approach of Farina et al. by means of a new decomposition of correlated strategies which allows players to re-optimize their sequence-form strategies with respect to correlation plans which were previously added to the support. Our techniques outperform the prior state of the art for computing optimal general-sum correlated equilibria. For team games, the two-sided column generation approach vastly outperforms standard column generation approaches, making it the state of the art algorithm when the parameter is large. Along the way we also introduce two new benchmark games: a trick-taking game that emulates the endgame phase of the card game bridge, and a ride-sharing game.