Online DCM Trajectory Generation for Push Recovery of Torque-Controlled Humanoid Robots
Paper and Code
Oct 14, 2019
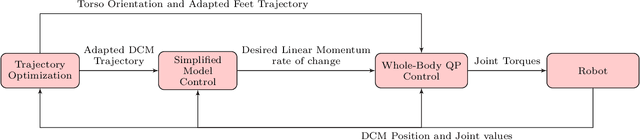
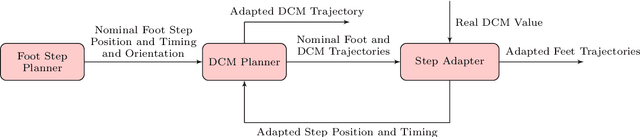

We present a computationally efficient method for online planning of bipedal walking trajectories with push recovery. In particular, the proposed methodology fits control architectures where the Divergent-Component-of-Motion (DCM) is planned beforehand, and adds a step adapter to adjust the planned trajectories and achieve push recovery. Assuming that the robot is in a single support state, the step adapter generates new positions and timings for the next step. The step adapter is active in single support phases only, but the proposed torque-control architecture considers double support phases too. The key idea for the design of the step adapter is to impose both initial and final DCM step values using an exponential interpolation of the time varying ZMP trajectory.This allows us to cast the push recovery problem as a Quadratic Programming (QP) one, and to solve it online with state-of-the-art optimisers. The overall approach is validated with simulations of the torque-controlled 33 kg humanoid robot iCub. Results show that the proposed strategy prevents the humanoid robot from falling while walking at 0.28 m/s and pushed with external forces up to 150 Newton for 0.05 seconds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge