Online Acoustic System Identification Exploiting Kalman Filtering and an Adaptive Impulse Response Subspace Model
Paper and Code
May 07, 2021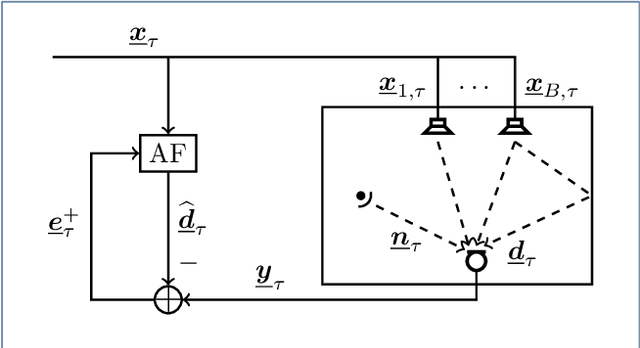
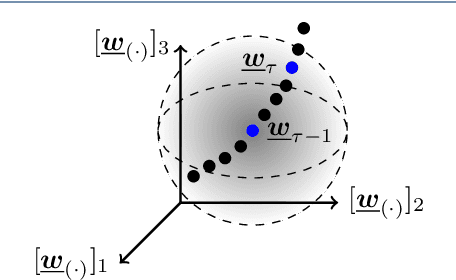
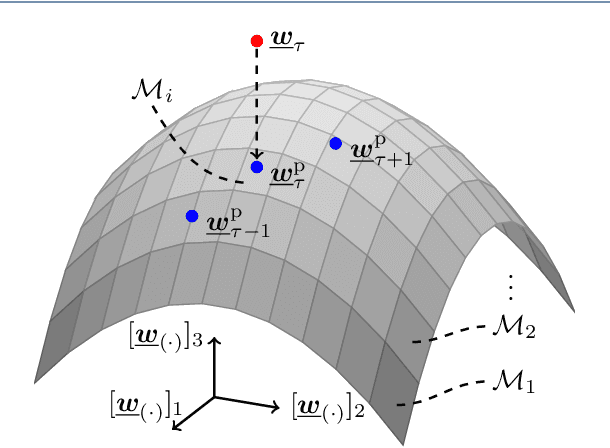
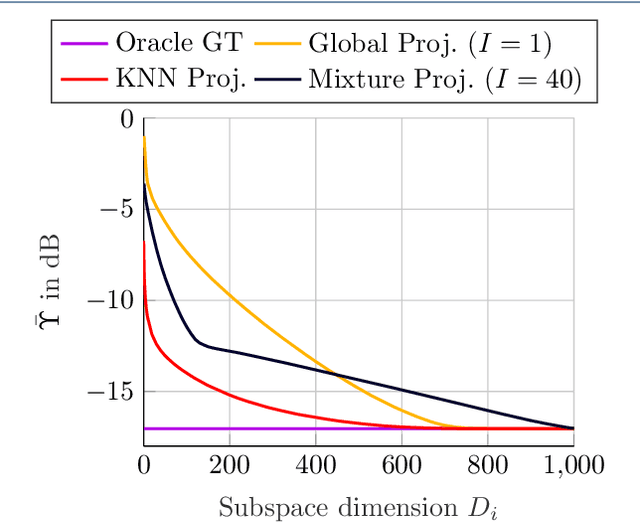
We introduce a novel algorithm for online estimation of acoustic impulse responses (AIRs) which allows for fast convergence by exploiting prior knowledge about the fundamental structure of AIRs. The proposed method assumes that the variability of AIRs of an acoustic scene is confined to a low-dimensional manifold which is embedded in a high-dimensional space of possible AIR estimates. We discuss various approaches to locally approximate the AIR manifold by affine subspaces which are assumed to be tangential hyperplanes to the manifold. The validity of these model assumptions is verified for simulated data. Subsequently, we describe how the learned models can be used to improve online AIR estimates by projecting them onto an adaptively estimated subspace. The parameters determining the subspace are learned from training samples in a local neighbourhood to the current AIR estimate. This allows the system identification algorithm to benefit from preceding estimates in the acoustic scene. To assess the proximity of training data AIRs to the current AIR estimate, we introduce a probabilistic extension of the Euclidean distance which improves the performance for applications with correlated excitation signals. Furthermore, we describe how model imperfections can be tackled by a soft projection of the AIR estimates. The proposed algorithm exhibits significantly faster convergence properties in comparison to a high-performance state-of-the-art algorithm. Furthermore, we show an improved steady-state performance for speech-excited system identification scenarios suffering from high-level interfering noise and nonunique solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge