On the Role of Optimization in Double Descent: A Least Squares Study
Paper and Code
Jul 27, 2021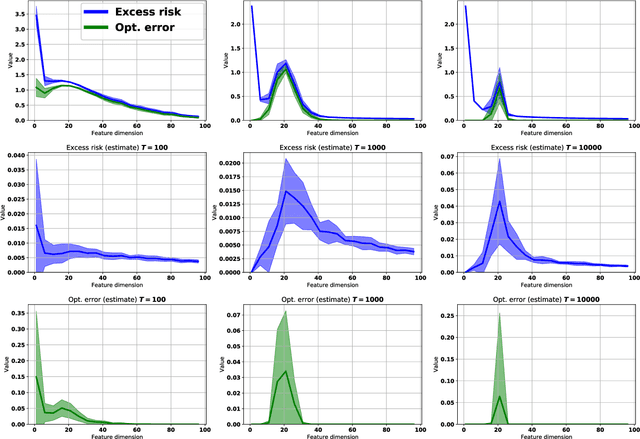
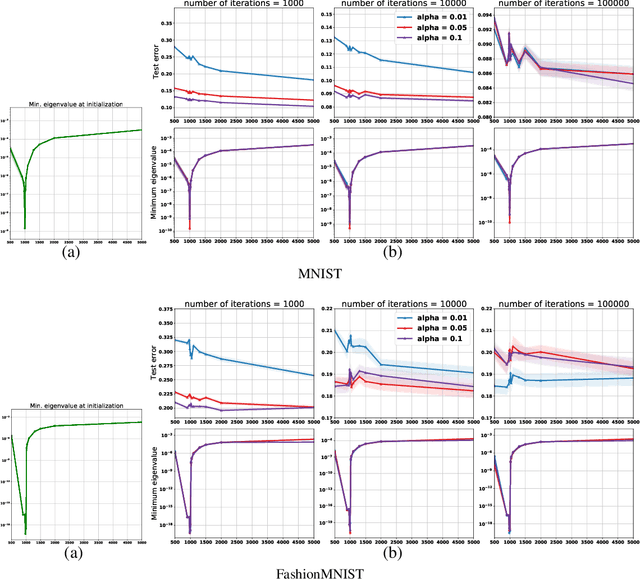
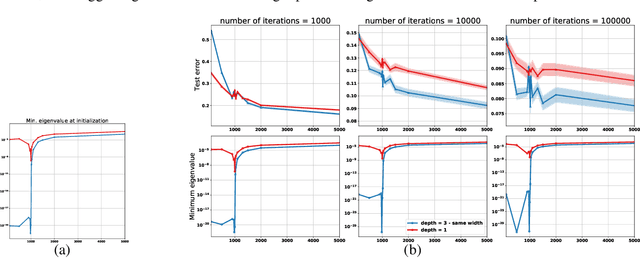
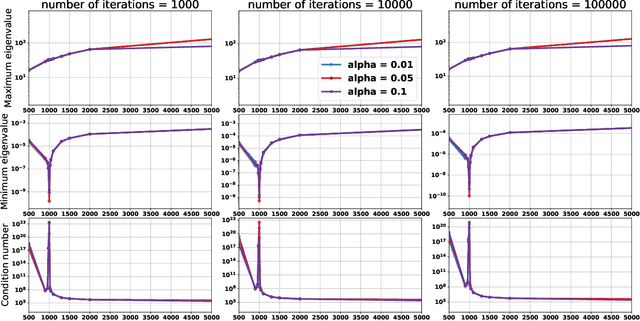
Empirically it has been observed that the performance of deep neural networks steadily improves as we increase model size, contradicting the classical view on overfitting and generalization. Recently, the double descent phenomena has been proposed to reconcile this observation with theory, suggesting that the test error has a second descent when the model becomes sufficiently overparameterized, as the model size itself acts as an implicit regularizer. In this paper we add to the growing body of work in this space, providing a careful study of learning dynamics as a function of model size for the least squares scenario. We show an excess risk bound for the gradient descent solution of the least squares objective. The bound depends on the smallest non-zero eigenvalue of the covariance matrix of the input features, via a functional form that has the double descent behavior. This gives a new perspective on the double descent curves reported in the literature. Our analysis of the excess risk allows to decouple the effect of optimization and generalization error. In particular, we find that in case of noiseless regression, double descent is explained solely by optimization-related quantities, which was missed in studies focusing on the Moore-Penrose pseudoinverse solution. We believe that our derivation provides an alternative view compared to existing work, shedding some light on a possible cause of this phenomena, at least in the considered least squares setting. We empirically explore if our predictions hold for neural networks, in particular whether the covariance of intermediary hidden activations has a similar behavior as the one predicted by our derivations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge