On the Relationship between Online Gaussian Process Regression and Kernel Least Mean Squares Algorithms
Paper and Code
Sep 11, 2016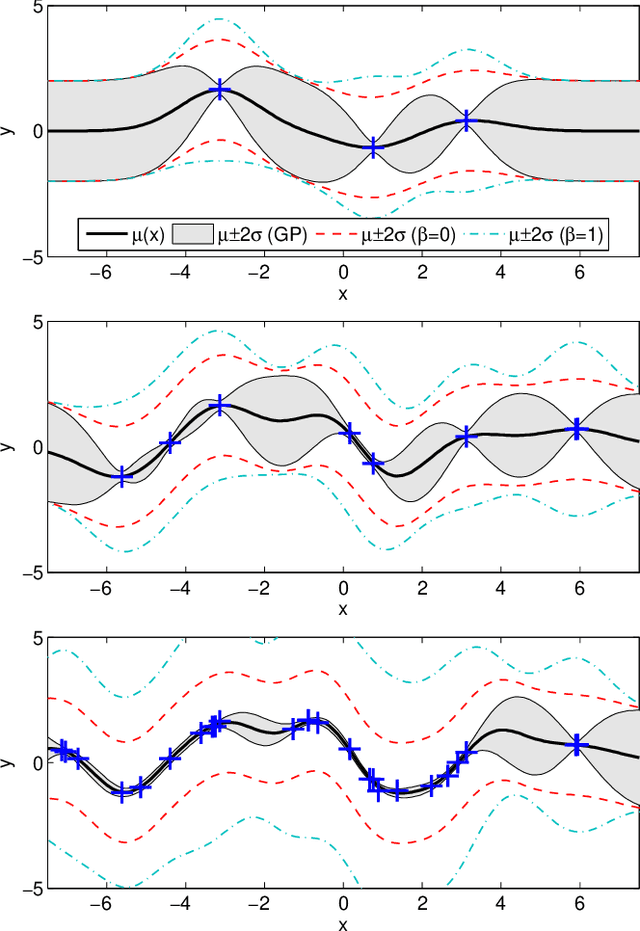
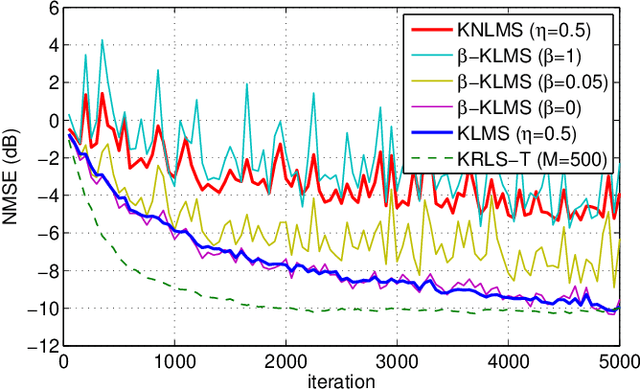
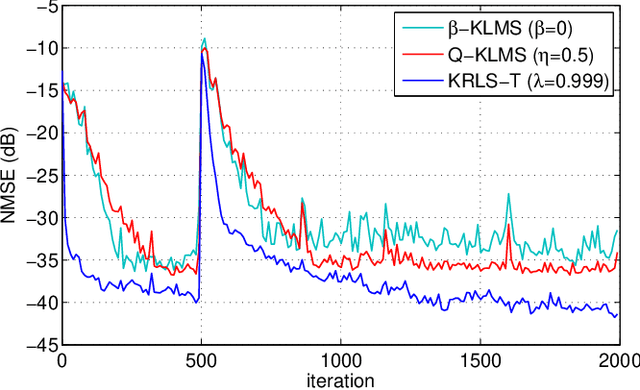
We study the relationship between online Gaussian process (GP) regression and kernel least mean squares (KLMS) algorithms. While the latter have no capacity of storing the entire posterior distribution during online learning, we discover that their operation corresponds to the assumption of a fixed posterior covariance that follows a simple parametric model. Interestingly, several well-known KLMS algorithms correspond to specific cases of this model. The probabilistic perspective allows us to understand how each of them handles uncertainty, which could explain some of their performance differences.
* Accepted for publication in 2016 IEEE International Workshop on
Machine Learning for Signal Processing
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge