On the Nonlinearity of Layer Normalization
Paper and Code
Jun 03, 2024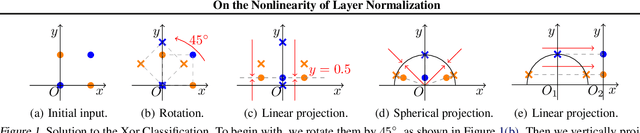
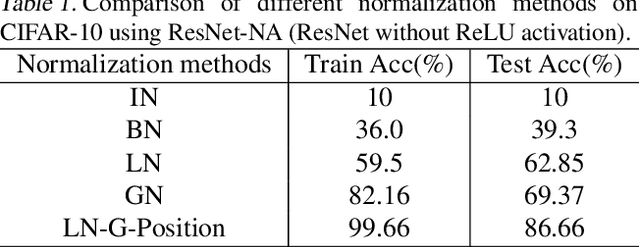
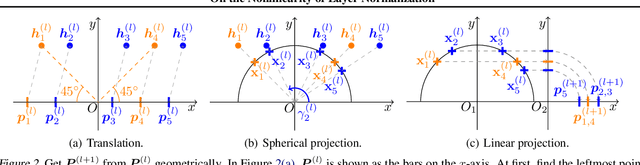
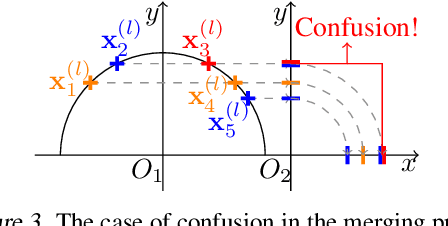
Layer normalization (LN) is a ubiquitous technique in deep learning but our theoretical understanding to it remains elusive. This paper investigates a new theoretical direction for LN, regarding to its nonlinearity and representation capacity. We investigate the representation capacity of a network with layerwise composition of linear and LN transformations, referred to as LN-Net. We theoretically show that, given $m$ samples with any label assignment, an LN-Net with only 3 neurons in each layer and $O(m)$ LN layers can correctly classify them. We further show the lower bound of the VC dimension of an LN-Net. The nonlinearity of LN can be amplified by group partition, which is also theoretically demonstrated with mild assumption and empirically supported by our experiments. Based on our analyses, we consider to design neural architecture by exploiting and amplifying the nonlinearity of LN, and the effectiveness is supported by our experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge