On the Mathematical Understanding of ResNet with Feynman Path Integral
Paper and Code
Apr 16, 2019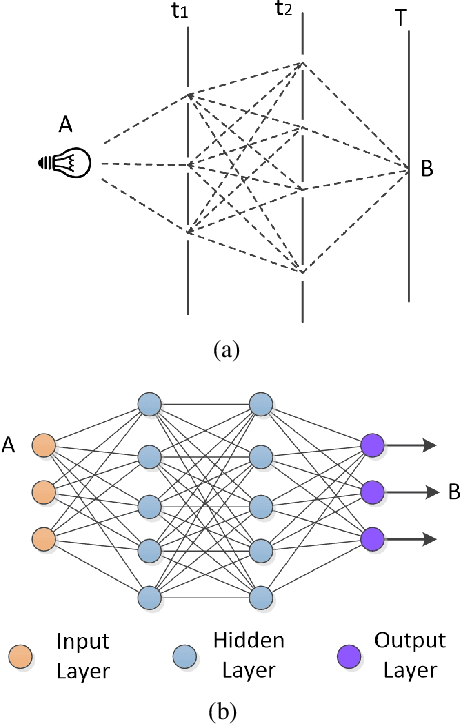

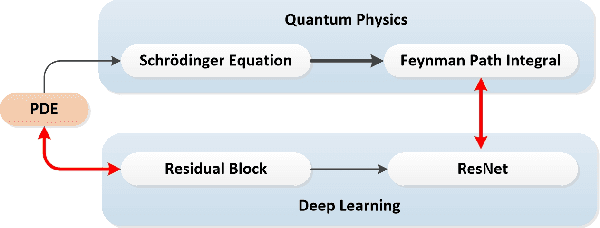

In this paper, we aim to understand Residual Network (ResNet) in a scientifically sound way by providing a bridge between ResNet and Feynman path integral. In particular, we prove that the effect of residual block is equivalent to partial differential equation, and the ResNet transforming process can be equivalently converted to Feynman path integral. These conclusions greatly help us mathematically understand the advantage of ResNet in addressing the gradient vanishing issue. More importantly, our analyses offer a path integral view of ResNet, and demonstrate that the output of certain network can be obtained by adding contributions of all paths. Moreover, the contribution of each path is proportional to e^{-S}, where S is the action given by time integral of Lagrangian L. This lays the solid foundation in the understanding of ResNet, and provides insights in the future design of convolutional neural network architecture. Based on these results, we have designed the network using partial differential operators, which further validates our theoritical analyses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge