On the Linear Belief Compression of POMDPs: A re-examination of current methods
Paper and Code
Aug 05, 2015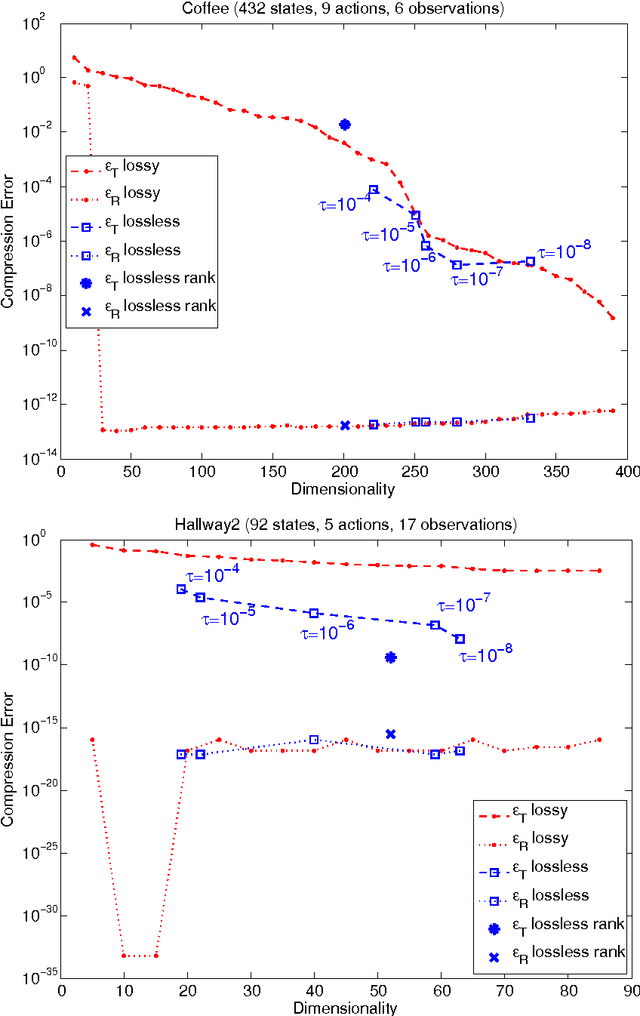
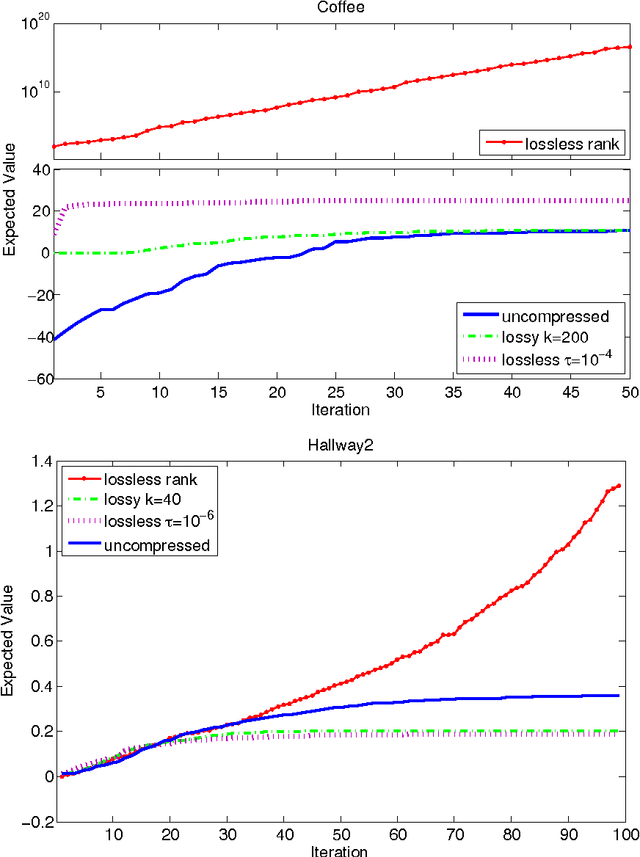
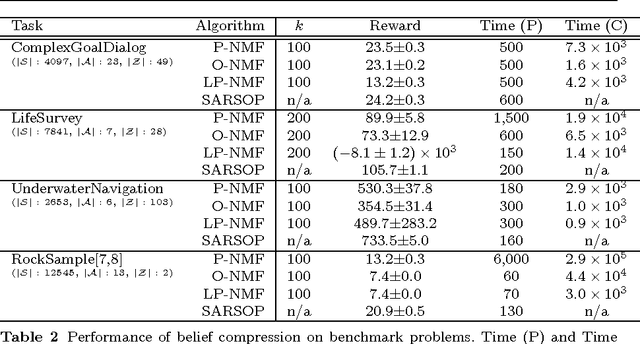
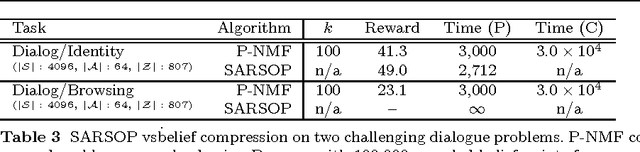
Belief compression improves the tractability of large-scale partially observable Markov decision processes (POMDPs) by finding projections from high-dimensional belief space onto low-dimensional approximations, where solving to obtain action selection policies requires fewer computations. This paper develops a unified theoretical framework to analyse three existing linear belief compression approaches, including value-directed compression and two non-negative matrix factorisation (NMF) based algorithms. The results indicate that all the three known belief compression methods have their own critical deficiencies. Therefore, projective NMF belief compression is proposed (P-NMF), aiming to overcome the drawbacks of the existing techniques. The performance of the proposed algorithm is examined on four POMDP problems of reasonably large scale, in comparison with existing techniques. Additionally, the competitiveness of belief compression is compared empirically to a state-of-the-art heuristic search based POMDP solver and their relative merits in solving large-scale POMDPs are investigated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge