On the Intrinsic Dimensionality of Face Representation

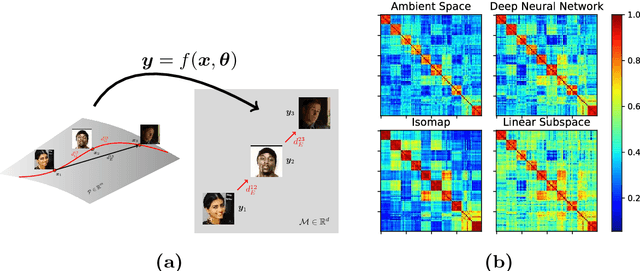
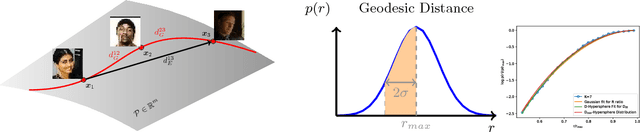
The two underlying factors that determine the efficacy of face representations are, the embedding function to represent a face image and the dimensionality of the representation, e.g. the number of features. While the design of the embedding function has been well studied, relatively little is known about the compactness of such representations. For instance, what is the minimal number of degrees of freedom or intrinsic dimensionality of a given face representation? Can we find a mapping from the ambient representation to this minimal intrinsic space that retains it's full utility? This paper addresses both of these questions. Given a face representation, (1) we leverage intrinsic geodesic distances induced by a neighborhood graph to empirically estimate it's intrinsic dimensionality, (2) develop a neural network based non-linear mapping that transforms the ambient representation to the minimal intrinsic space of that dimensionality, and (3) validate the veracity of the mapping through face matching in the intrinsic space. Experiments on benchmark face datasets (LFW, IJB-A, IJB-B, PCSO and CASIA) indicate that, (1) the intrinsic dimensionality of deep neural network representation is significantly lower than the dimensionality of the ambient features. For instance, Facenet's 128-d representation has an intrinsic dimensionality in the range of 9-12, and (2) the neural network based mapping is able to provide face representations of significantly lower dimensionality while being as discriminative (TAR @ 0.1% FAR of 84.67%, 90.40% at 10 and 20 dimensions, respectively vs 95.50% at 128 ambient dimension on the LFW dataset) as the corresponding ambient representation.