On the Independence Assumption in Neurosymbolic Learning
Paper and Code
Apr 12, 2024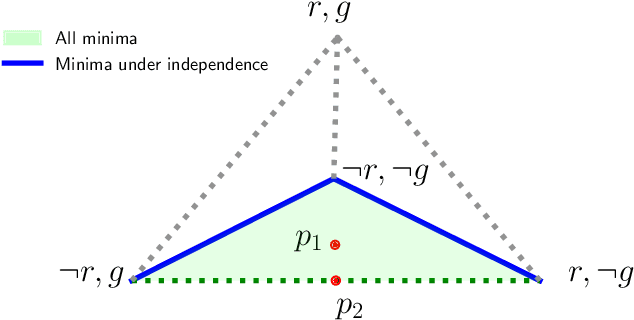

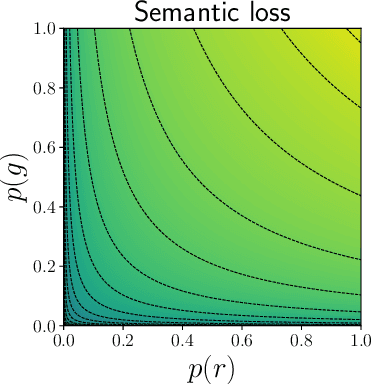
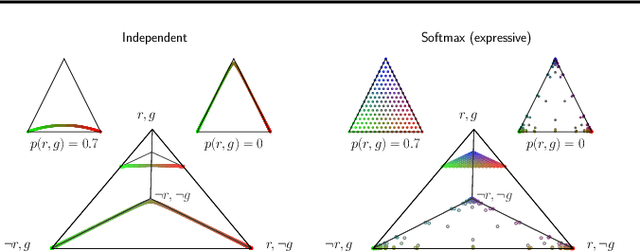
State-of-the-art neurosymbolic learning systems use probabilistic reasoning to guide neural networks towards predictions that conform to logical constraints over symbols. Many such systems assume that the probabilities of the considered symbols are conditionally independent given the input to simplify learning and reasoning. We study and criticise this assumption, highlighting how it can hinder optimisation and prevent uncertainty quantification. We prove that loss functions bias conditionally independent neural networks to become overconfident in their predictions. As a result, they are unable to represent uncertainty over multiple valid options. Furthermore, we prove that these loss functions are difficult to optimise: they are non-convex, and their minima are usually highly disconnected. Our theoretical analysis gives the foundation for replacing the conditional independence assumption and designing more expressive neurosymbolic probabilistic models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge