On the Effectiveness of Low-Rank Matrix Factorization for LSTM Model Compression
Paper and Code
Aug 27, 2019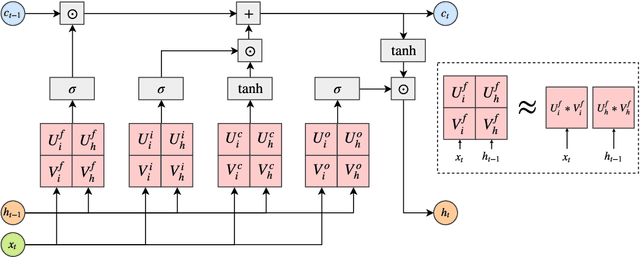
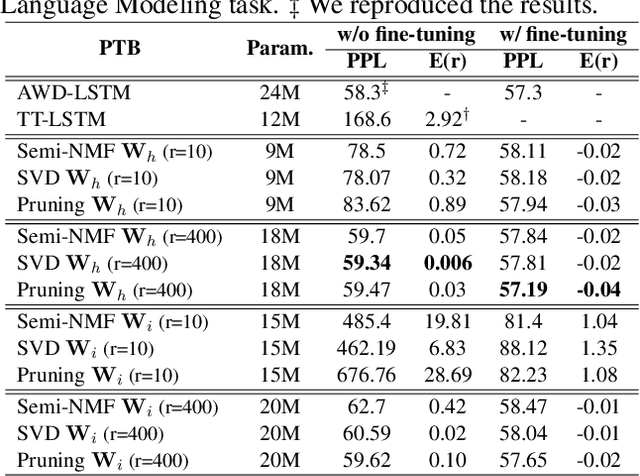
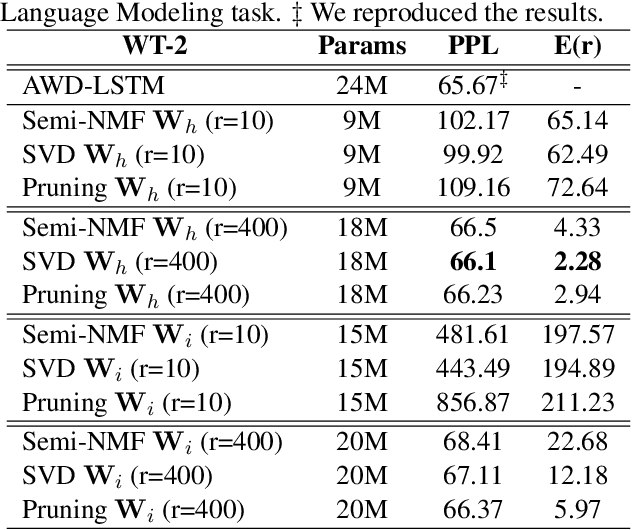
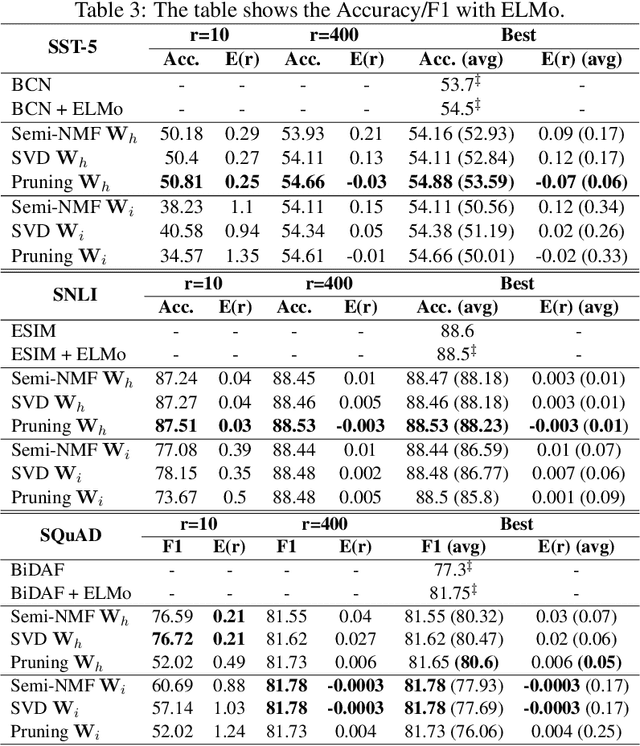
Despite their ubiquity in NLP tasks, Long Short-Term Memory (LSTM) networks suffer from computational inefficiencies caused by inherent unparallelizable recurrences, which further aggravates as LSTMs require more parameters for larger memory capacity. In this paper, we propose to apply low-rank matrix factorization (MF) algorithms to different recurrences in LSTMs, and explore the effectiveness on different NLP tasks and model components. We discover that additive recurrence is more important than multiplicative recurrence, and explain this by identifying meaningful correlations between matrix norms and compression performance. We compare our approach across two settings: 1) compressing core LSTM recurrences in language models, 2) compressing biLSTM layers of ELMo evaluated in three downstream NLP tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge