On the duality between contrastive and non-contrastive self-supervised learning

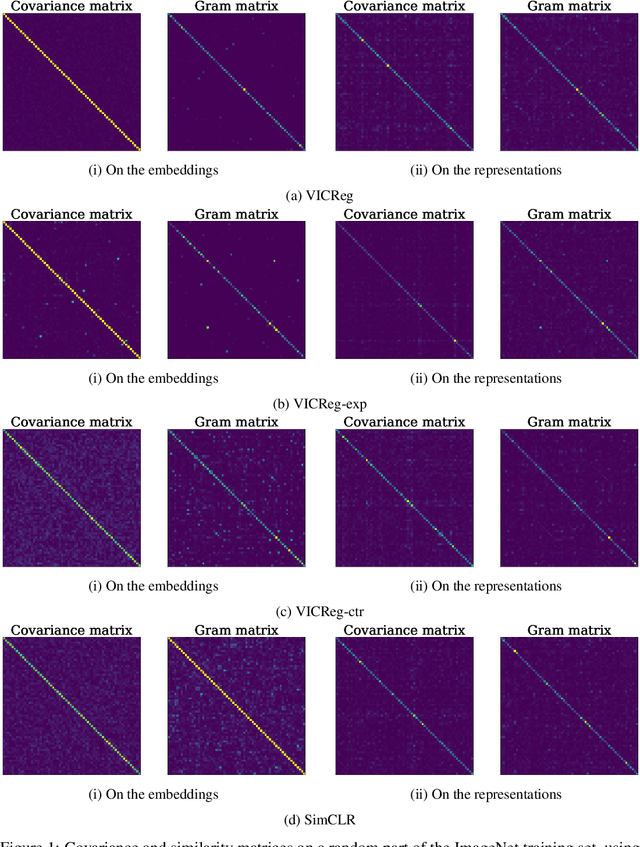
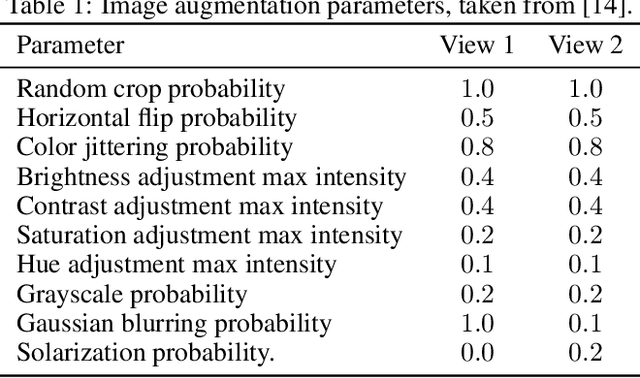
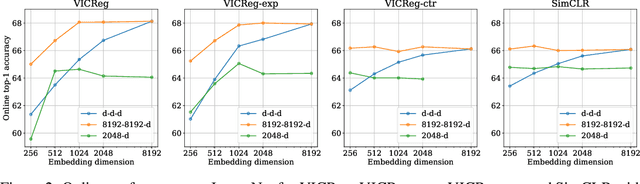
Recent approaches in self-supervised learning of image representations can be categorized into different families of methods and, in particular, can be divided into contrastive and non-contrastive approaches. While differences between the two families have been thoroughly discussed to motivate new approaches, we focus more on the theoretical similarities between them. By designing contrastive and non-contrastive criteria that can be related algebraically and shown to be equivalent under limited assumptions, we show how close those families can be. We further study popular methods and introduce variations of them, allowing us to relate this theoretical result to current practices and show how design choices in the criterion can influence the optimization process and downstream performance. We also challenge the popular assumptions that contrastive and non-contrastive methods, respectively, need large batch sizes and output dimensions. Our theoretical and quantitative results suggest that the numerical gaps between contrastive and noncontrastive methods in certain regimes can be significantly reduced given better network design choice and hyperparameter tuning.