On the Capacity of Face Representation

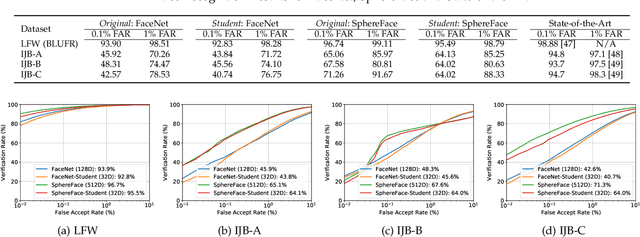
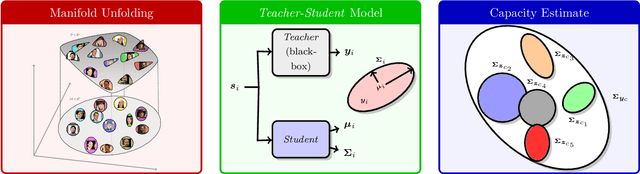
Face recognition is a widely used technology with numerous large-scale applications, such as surveillance, social media and law enforcement. There has been tremendous progress in face recognition accuracy over the past few decades, much of which can be attributed to deep learning-based approaches during the last five years. Indeed, automated face recognition systems are now believed to surpass human performance in some scenarios. Despite this progress, a crucial question still remains unanswered: given a face representation, how many identities can it resolve? In other words, what is the capacity of the face representation? A scientific basis for estimating the capacity of a given face representation will not only benefit the evaluation and comparison of different face representations but will also establish an upper bound on the scalability of an automatic face recognition system. We cast the face capacity estimation problem under the information theoretic framework of capacity of a Gaussian noise channel. By explicitly accounting for two sources of representational noise: epistemic uncertainty and aleatoric variability, our approach is able to estimate the capacity of any given face representation. To demonstrate the efficacy of our approach, we estimate the capacity of a 128-dimensional DNN based face representation, FaceNet, and that of the classical Eigenfaces representation of the same dimensionality. Our experiments on unconstrained faces indicate that, (a) our proposed model yields a capacity upper bound of 5.8x$10^{8}$ for FaceNet and 1x$10^{0}$ for Eigenfaces at a false acceptance rate (FAR) of 1%, (b) the face representation capacity reduces drastically as you lower the desired FAR (for FaceNet; the capacity at FAR of 0.1% and 0.001% is 2.4x$10^{6}$ and 7.0x$10^{2}$, respectively), and (c) the empirical performance of FaceNet is significantly below the theoretical limit.