On Regularization and Robustness of Deep Neural Networks

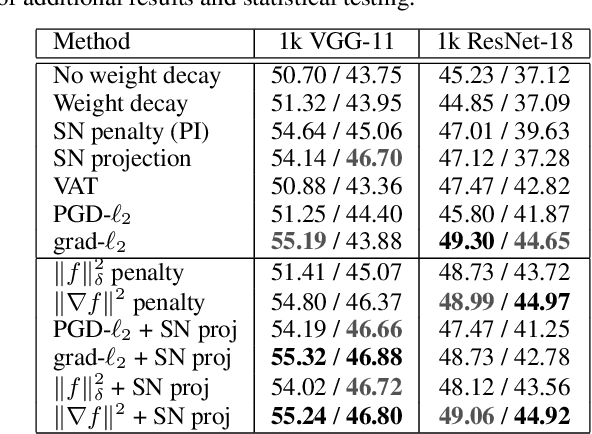
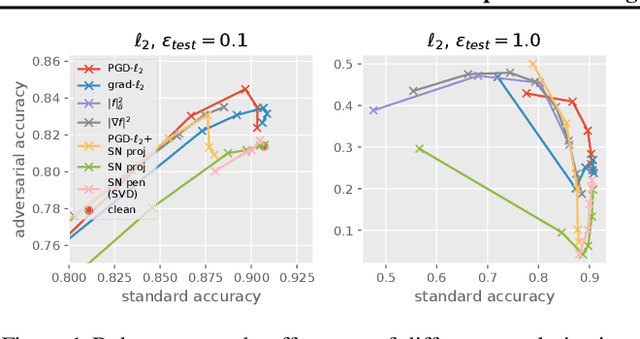
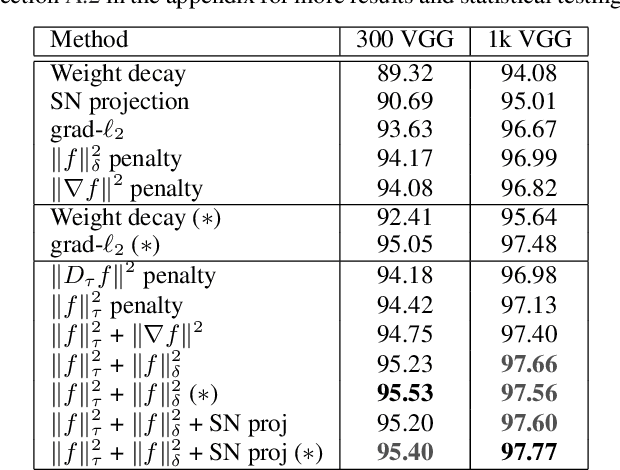
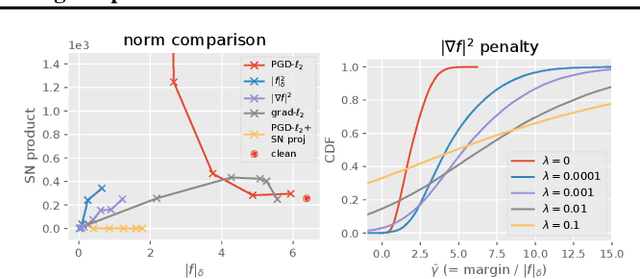
Despite their success, deep neural networks suffer from several drawbacks: they lack robustness to small changes of input data known as "adversarial examples" and training them with small amounts of annotated data is challenging. In this work, we study the connection between regularization and robustness by viewing neural networks as elements of a reproducing kernel Hilbert space (RKHS) of functions and by regularizing them using the RKHS norm. Even though this norm cannot be computed, we consider various approximations based on upper and lower bounds. These approximations lead to new strategies for regularization, but also to existing ones such as spectral norm penalties or constraints, gradient penalties, or adversarial training. Besides, the kernel framework allows us to obtain margin-based bounds on adversarial generalization. We study the obtained algorithms for learning on small datasets, learning adversarially robust models, and discuss implications for learning implicit generative models.