On-line Joint Limit Avoidance for Torque Controlled Robots by Joint Space Parametrization
Paper and Code
Jul 26, 2017
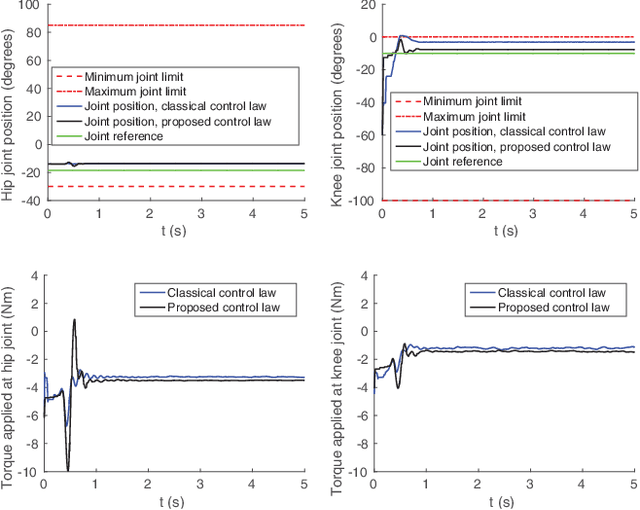
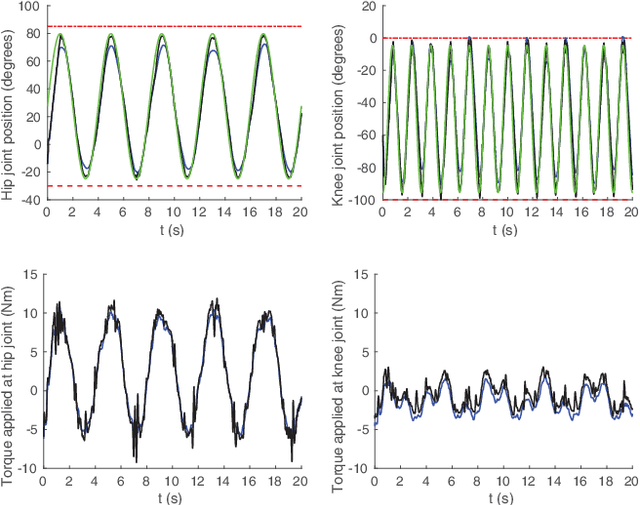
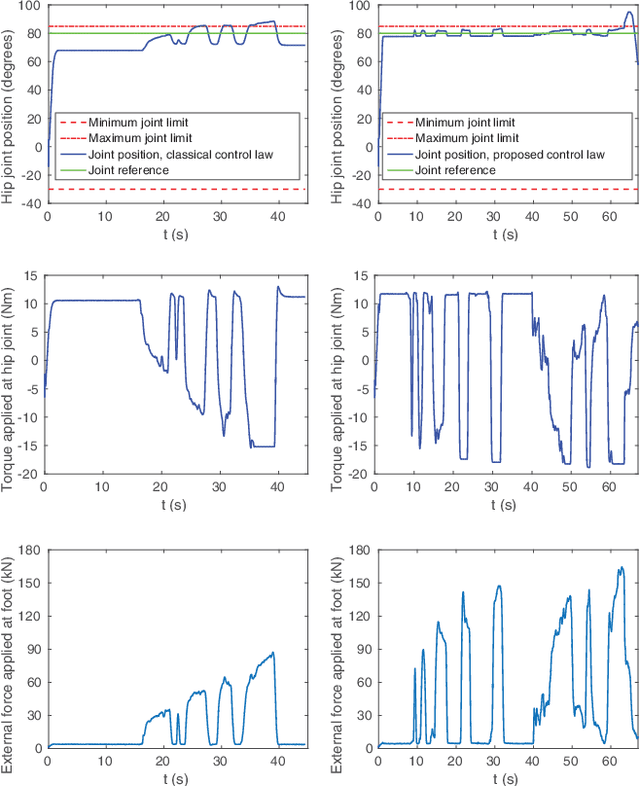
This paper proposes control laws ensuring the stabilization of a time-varying desired joint trajectory, as well as joint limit avoidance, in the case of fully-actuated manipulators. The key idea is to perform a parametrization of the feasible joint space in terms of exogenous states. It follows that the control of these states allows for joint limit avoidance. One of the main outcomes of this paper is that position terms in control laws are replaced by parametrized terms, where joint limits must be avoided. Stability and convergence of time-varying reference trajectories obtained with the proposed method are demonstrated to be in the sense of Lyapunov. The introduced control laws are verified by carrying out experiments on two degrees-of-freedom of the humanoid robot iCub.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge