On Generalization for Generative Flow Networks
Paper and Code
Jul 03, 2024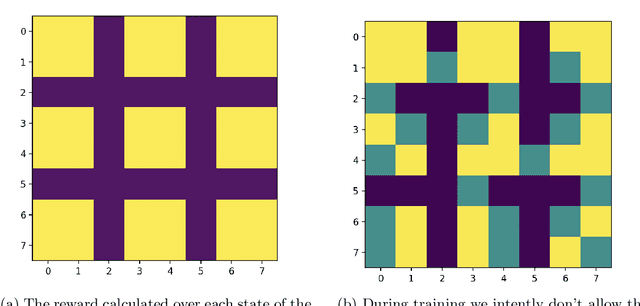
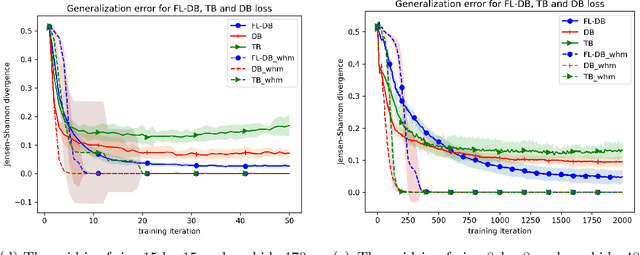
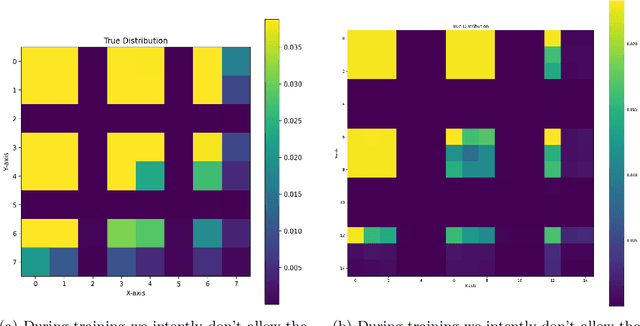
Generative Flow Networks (GFlowNets) have emerged as an innovative learning paradigm designed to address the challenge of sampling from an unnormalized probability distribution, called the reward function. This framework learns a policy on a constructed graph, which enables sampling from an approximation of the target probability distribution through successive steps of sampling from the learned policy. To achieve this, GFlowNets can be trained with various objectives, each of which can lead to the model s ultimate goal. The aspirational strength of GFlowNets lies in their potential to discern intricate patterns within the reward function and their capacity to generalize effectively to novel, unseen parts of the reward function. This paper attempts to formalize generalization in the context of GFlowNets, to link generalization with stability, and also to design experiments that assess the capacity of these models to uncover unseen parts of the reward function. The experiments will focus on length generalization meaning generalization to states that can be constructed only by longer trajectories than those seen in training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge