On Focal Loss for Class-Posterior Probability Estimation: A Theoretical Perspective
Paper and Code
Dec 14, 2020
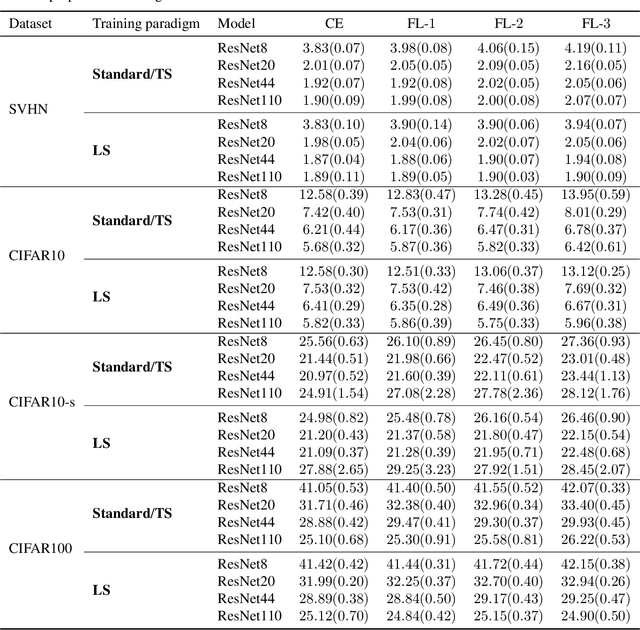
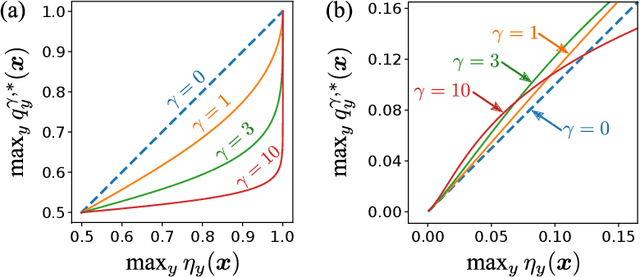
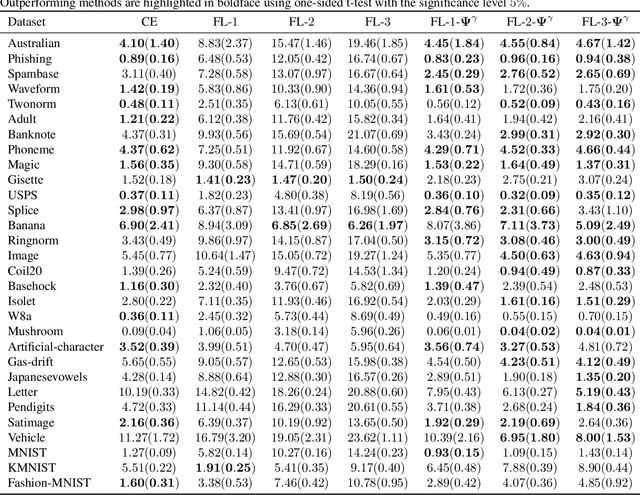
The focal loss has demonstrated its effectiveness in many real-world applications such as object detection and image classification, but its theoretical understanding has been limited so far. In this paper, we first prove that the focal loss is classification-calibrated, i.e., its minimizer surely yields the Bayes-optimal classifier and thus the use of the focal loss in classification can be theoretically justified. However, we also prove a negative fact that the focal loss is not strictly proper, i.e., the confidence score of the classifier obtained by focal loss minimization does not match the true class-posterior probability and thus it is not reliable as a class-posterior probability estimator. To mitigate this problem, we next prove that a particular closed-form transformation of the confidence score allows us to recover the true class-posterior probability. Through experiments on benchmark datasets, we demonstrate that our proposed transformation significantly improves the accuracy of class-posterior probability estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge